Abstract
Orientation: Value-at-risk (VAR) and other risk management tools, such as expected shortfall (conditional VAR), are heavily reliant on a suitable set of underlying distributional conjecture. Thus, distinguishing the underlying distribution that best captures all properties of stock returns is of great interest to both scholars and risk managers.
Research purpose: Comparing the execution of the generalised auto-regressive conditional heteroscedasticity (GARCH)-type model combined with heavy-tailed distributions, namely the Student’s t-distribution, Pearson type-IV distribution (PIVD), generalised Pareto distribution (GPD) and stable distribution (SD), in estimating VAR of Johannesburg Stock Exchange (JSE) All Share Price Index (ALSI) returns.
Motivation for the study: The proposed models have the potential to apprehend volatility clustering and the leverage effect through the GARCH scheme and at the same time model the heavy-tailed behaviour of the financial returns.
Research approach/design and method: The GARCH-type model combined with heavy-tailed distributions, namely the Student’s t-distribution, PIVD, GPD and SD, is developed to estimate VAR of JSE ALSI returns. The model performances are assessed through Kupiec likelihood ratio test.
Main findings: The results show that the asymmetric power auto-regressive conditional heteroscedastic models combined with GPD and PIVD are the robust VAR models for South African’s market risk.
Practical/managerial implications: The outcomes of this study are expected to be of salient value to financial analysts, portfolio managers, risk managers and financial market researchers, thus giving a better understanding of the South African financial market.
Contributions/value-add: Asymmetric power auto-regressive conditional heteroscedastic model combined with heavy-tailed distributions provides a good option for modelling stock returns.
Keywords: asymmetric volatility models; value-at-risk; heavy-tailed distributions; JSE All Share Index, backtesting.
Introduction
South Africa is one of the most diverse and promising emerging markets globally. It is the sixth most outstanding in the emerging economies category with vast opportunities within its border. It is a gateway to the rest of the African continent (a market of more than 1 billion people) and is a key investment location. It is the economic powerhouse of Africa and forms part of BRICS group of countries, which includes Brazil, Russia, India and China. South African stock market, Johannesburg Stock Exchange (JSE), is the largest stock exchange in Africa with more than 400 listed firms offering a wide range of products. The South African stock market is significantly robust and is able to make the list of the first 20 largest stock markets in the world consistently (Hassan 2013). This market value is unavoidably significant among world stock indexes, making it respond to the global economic meltdown surrounding emerging markets.
The JSE All Share Index (ALSI) is crafted to represent the performance of South African companies, providing investors with a broad and harmonious set of indices, which compute the performance of the major capital and industry components of the South African stock market. It has 164 listed companies and it is about 99% of the capitalisation of the South African market. The ALSI as an equity index portrays the operational activities of a typical ordinary share in the South African market. The ALSI also evaluates the operationalisation of the entire market (Makhwiting 2014). The major volume of all securities listed on the JSE is an integral function of the market index because the share prices flow of the listed companies is what drives the market.
However, this market is highly volatile and unpredictable, making it very risky. This may be the result of stylised characteristics of financial returns that include volatility clustering, long-range dependency, time-varying volatility and non-normality (Fama 1965; Mandelbrot 1963; Stavroyiannis et al. 2012). Financial returns computed at the weekly, daily or higher frequency show the near-indelible attribute of conditional heteroscedasticity (Paolella 2016). The generalised auto-regressive conditional heteroscedasticity (GARCH)-type models, usually propelled by Gaussian innovations, result in a heavy-tailed process and the innovations are still highly non-Gaussian. Innumerable suggestions have been made for substituting the Gaussian distribution with a leptokurtic one, the ground-breaking article being Bollerslev (1987) with the use of a Student’s t-distribution. Bhattacharyya, Chaudhary and Yadav (2008) used a GARCH (1,1) combined with Pearson type-IV distribution (PIVD) to model volatility clustering of stock indices of countries in Europe and Asia. Chan and Gary (2006) employed a GARCH (1,1) combined with generalised extreme value distribution to model electricity spot prices.
There are many types of empirical models that have been used to describe the stylised facts in stock returns. These include: the auto-regressive conditional heteroscedasticity (ARCH) model proposed by Engle (1982), the GARCH model of Bollerslev (1986), the integrated GARCH (IGARCH) model of Engle and Bollerslev (1986), the exponential GARCH (EGARCH) model of Nelson (1991), the threshold GARCH (TGARCH) model of Glosten, Jagannathan and Runkle (1993), the asymmetric power ARCH (APARCH) model proposed by Ding Granger and Engle (1993), the long memory models such as the fractionally integrated GARCH (FIGARCH) model of Baillie, Bollerslev and Mikkelsen (1996), the fractionally integrated exponential GARCH (FIEGARCH) model of Bollerslev and Mikkelsen (1996), the fractionally integrated APARCH (FIAPARCH) model of Tse (1998) and the hyperbolic GARCH (HYGARCH) model proposed by Davidson (2004). To obtain good estimates for risk management, the challenge is to choose the appropriate GARCH-type model which adequately captures volatility clustering and at the same time is able to capture the non-normality property of financial returns. Paolella (2016) used stable APARCH model to model four stocks from DJIA index. Sin, Cheong and Hooi (2017) used the TGARCH combined with the generalised error distribution (GED) to model crude oil index. In the literature, there is no agreement of the type of the heavy-tailed distribution to be used in order to capture the non-normality of the residuals of the GARCH-type models. In this article, we are interested in the relative performance of the APARCH model combined with heavy-tailed distributions, namely generalised Pareto distribution (GPD), PIVD and stable distributions (SDs) in estimating the value-at-risk (VAR) for South Africa stock market.
We are not aware of any literature relating to an application of APARCH-GPD model, APARCH-PIVD model and APARCH-SD model to the JSE ALSI. To the best of our knowledge, there is limited research on combining dynamic volatility models with heavy-tailed distributions in modelling South African financial data. In this article, we extend the work of Paolella (2016) by proposing GARCH-type models combined with heavy-tailed distributions to model the daily JSE All Share Price returns. We estimate VAR and then select the more robust model using the Kupiec likelihood ratio (LR) test.
The rest of the article is organised as follows. In Section 2, we provide some background theory on APARCH(1,1), GPD, PIVD, SD, VAR and backtesting. The data used in this study are described in Section 3. In Section 4, we present the empirical results and discussions. Finally, Section 5 concludes this work.
Methodology
In this section, we present some background theory on the APARCH (1,1) model combined with GPD, PIVD and SDs. We also discuss VAR and backtesting procedures.
Asymmetric power auto-regressive conditional heteroscedastic (1,1) model
Ding et al. (1993) introduced the APARCH model as an extension of the GARCH model. The APARCH generalised both the ARCH and GARCH models. The general APARCH (p, q) model can be written as:
Where εt is assumed to follow a distribution with mean zero and variance 1, ω > 0, αi ≥ 0, βj ≥ 0 and  . αi and βj are the ARCH and GARCH coefficients, respectively, and γi is the leverage coefficient. When γi is positive, it implies that the negative shocks have stronger impact on price volatility than the positive shocks. δ is a positive real number that functions as the symmetric power transformation of σt. Considering the case where δ = 1 for p = q = 1, the volatility equation becomes:
Maximum likelihood estimation
In estimating the parameters of the GARCH-type models, the maximum likelihood estimation (MLE) method is the most common method for the estimation of GARCH model (Karlsson 2002; Shabani, Gharneh & Esfahanipour 2017). Let L(η | X1, X2,…, XT) be the likelihood function, where η = (γ, δ, θ) are the set of parameters needed to be estimated in the case of the APARCH (p, q) model, where γ and q are defined as γ = (γ1, γ2 …, γp) and γ = (ω, α1, …, αp, β1 …, βp). Also, given that the data X1, X2,…, XT are not independent, then the joint density function is given by:
where Ft is information at time t and f is the density function of εt.
The likelihood function can be written as:
Then, the log-likelihood function is:
Generalised Pareto distribution
The two-parameter GPD, with scale parameter β and shape parameter ξ, has the following distribution function:
where y = x–τ are the exceedances above the threshold τ and y > 0 when, ξ ≥ 0, 0 ≤ y ≤ –β/ξ when ξ < 0, and the scale parameter β > 0 (Tsay, 2013).
Peaks-over-threshold
In order to fit the GPD to standardised residuals, we used the peaks-over-threshold (POT) method. The POT method establishes extreme data points (i.e. extreme standardised residuals) that go beyond a high threshold τ and specifically models these exceedances separately from non-extreme data points. For x–τ ≥ 0, the excess distribution function is written as:
which can also be expressed as:
which permits us to apply the POT method (Chinhamu et al. 2014). To apply the POT method in modelling, there are mainly two steps to follow. Firstly, we need to choose a suitable threshold. Secondly, we fit the GPD to the exceedances. For a sufficiently high threshold, F(τ) is estimated by (1–Nτ/n), where n is the sample size and Nτ is the number exceedances. According to Embrechts et al. (2013), Ft(x–t) can be estimated by a GPD approximation using MLE procedure. The tail estimator obtained is given by:
The choice of threshold, τ, is an act of balancing bias and variance (Chinhamu et al. 2014). If the threshold is too low, it is more likely to violate the asymptotic property of the model and cause bias; if the threshold is too high, it will generate a small number of exceedances for fitting and results in high variances. A fundamental approach is to select a threshold as low as possible such that the estimation of the model can provide a rational result (Chinhamu et al. 2014; Ren & Giles 2007).
Threshold selection
In this article, we utilise the mean excess plot and the parameter stability plot for threshold selections.
Mean excess plot
Beirlant et al. (2004) define the mean excess function with the finite expectation E(X) <∞ as e(τ) = E(X −τ|X > τ), that is, the mean of exceedances over a threshold τ. If the latent distribution of X–τ |X > τ follows a GPD, it implies that the proportionate mean excess function is:
provided that  and ξ < 1. From [Eqn 9], it can be seen that the mean excess function is linear in τ. It implies that X > τ follows a GPD if and only if the mean excess function is linear in τ (Chinhamu et al. 2014; Coles 2001). The empirical mean excess function is defined as:
where n is the sample size and  is the indicator function. The empirical excess plot is a graphical representation of the paired observations. (τ, ê (τ)) (According to Coles (2001), the interpretation of the mean excess plot is not always simple in practice. The mean excess plot can be used to choose the suitable threshold τ. The suitable threshold is obtained when the graph shows some evidence of linearity.
Parameter stability plot
If GPD is true for excesses over threshold ’w’ with ɛ and σw then for higher threshold τ > w, these excesses also adopt a GPD with ɛ which has a scale parameter given by: στ = σw + ε (τ − w), by re-parameterising the scale parameter σt, σ* = σt − ετ which is constant with respect to τ, because w is positioned at a threshold of reasonably high value (Coles 2001). A parameter stability plot conforms GPD over specific values of the thresholds in contrast to the scale and shape parameters. The model threshold is selected at the spot where the shape and the scale parameter remain fixed even upon considering sampling variability. When a suitable threshold is obtained, the exceedance follows a GPD.
Maximum likelihood estimation for generalised Pareto distribution
For a sufficiently high threshold τ and assuming that there are m exceedances with Xi–τ ≥ 0, the subsample {x1 − τ, … ,xm − τ} has an underlying GPD distribution, where xi−τ ≥ 0 for ξ ≥ 0, 0 ≤ Xi−τ ≤ β/ξ for ξ < 0, and then the logarithm of the probability density function (pdf) of xi can be derived as:
Hence, the log-likelihood function L(ξ, β|yi − t ) for the GPD is the logarithm of the joint density of the m exceedances, that is,
To obtain the estimates for ξ and β, we maximise the log-likelihood function of the subsample under an optimal threshold τ.
Bartels’ rank test
Before we fit the GPD to the standardised residuals, we need to check whether they are independent and identically distributed (i.i.d) using the Bartels’ rank test. The Bartels’ rank test is based on the rank of standardised residuals in ascending order. The ranks are sequential number of xi: Rank (xi). All the possible set of rank arrangement of standardised residuals is given as n!. Under the null hypothesis of randomness, each rank arrangement is equally likely to occur. The test statistic is given as:
For large sample size, test statistics is:
Model fit diagnostic plot
Probability plot, return level plot, quantile plot and empirical versus fitted density comparison plots are part of standard statistical model diagnostic plots used in checking models fit as well as threshold choice suitability. Most of the checks are post-calculation diagnostic plots and are therefore based on a chosen threshold.
Pearson type-IV distribution
The generalised family of frequency curves, now known as the Pearsonian system of curves, was first developed by Karl Pearson (Cheng 2011). The Pearsonian family includes members such as the PTIVD, normal, Student-t, F, beta, gamma and inverse Gaussian, Pareto distributions. The pdf of the PIVD is given by:
where >1/2, υ > 0, a > 0, −∞ < x < ∞, λ are real-valued parameters and  is a normalisation constant that depends on m, v and a. The pdf of the PIVD is invariable under simultaneous change (a to − a, v to − v). We specify, a > 0, so that the curve is always bell-shaped. λ and a are the location and scale parameters, respectively, and υ is the skewness parameter. If υ > 0, then the distribution is positive, while if υ < 0, then the distribution is negative. The parameter m controls the tail thickness and can thus be regarded as a kurtosis parameter. If m is decreased, the kurtosis is increased and for smaller values of m, the tails of PIVD are heavier than those of a Gaussian distribution. The PIVD is essentially an asymmetric version of the Student-t distribution, that is, when υ = 0.
Maximum likelihood parameter estimation of the Pearson type-IV distribution
We obtain the parameter estimates of the PIVD by minimising the negative log-likelihood given by:
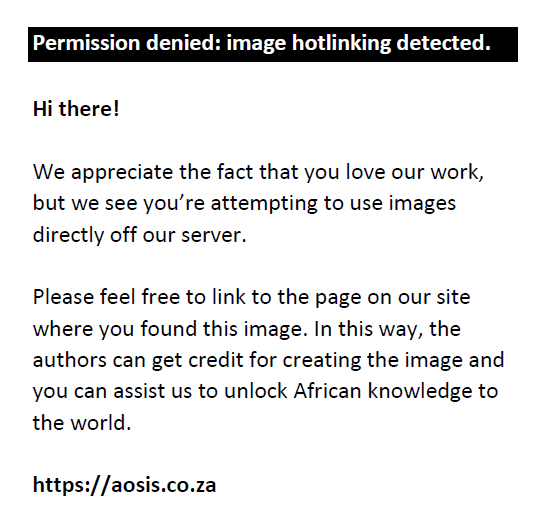
where N is the number of observed data points xi. The minimising procedure is performed numerically.
For more details on the MLE of the Pearson’s family distributions, see Johnson, Kotz and Balakrishman (1994) and Nagahara (1999). In this article, the maximum likelihood (ML) estimates for the PIVD are estimated using the R package (PearsonDS).
Stable distribution
The SD is a class of probability distributions described by four parameters, namely α an index of stability (shape parameter) with range 0 < α ≤ 2 (in the literature, α is also referred to as the shape parameter), υ the skewness parameter with range, −1 ≤ β ≤ 1, γ ≥ 0 the scale parameter and δ ϵ ℝ a location parameter. These distributions are widely used in practice because they allow for skewness and heavy tails. Although many parametrisations can be used to describe the characteristic function of an SD, it does not have an analytical form in general. We follow the S0-parametrisation suggested by Nolan (2014) and say a random variable X follows an SD if its characteristic function is given by:
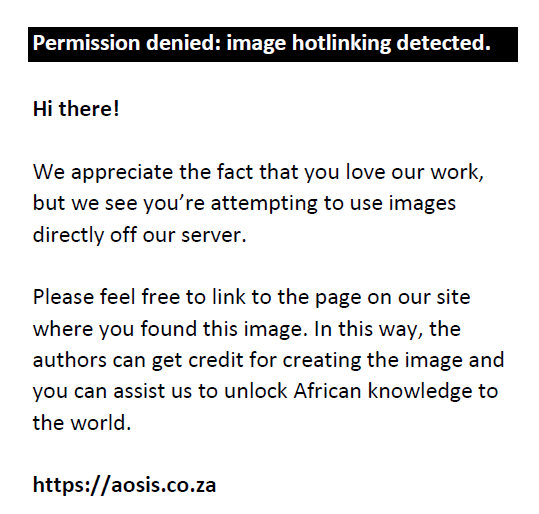
The sign function used in Eqn 15 is defined as:
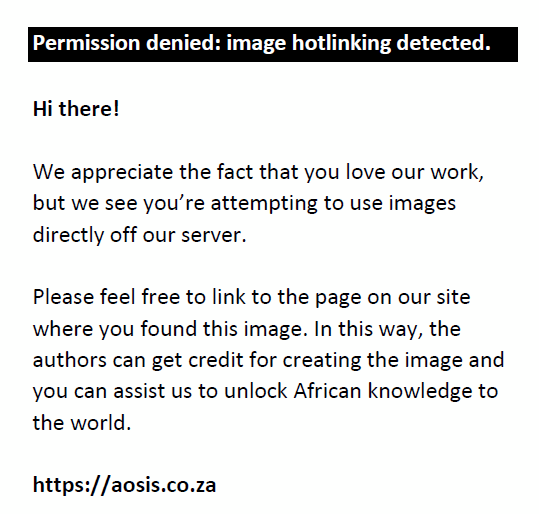
For the a = 1 case, x logx at x = 0 is interpreted as limx↓0xlogx=0.
Parameter estimation of stable distributions
The fundamental problem of estimation for SDs is to estimate the four parameters a, β, γ and δ. Many approaches have been used in estimating this basic problem; McCulloch (1986) proposed a quantile method; Ma and Nikias (1995) developed a fractional moment method, while sample characteristic function (SCF) method was introduced by Kogon and Williams (1998), which was a product of the foundation built by DuMouchel (1973) on MLE. Ojeda (2001) extensively compared these approaches where he concluded that ML estimates showed the most accurate measure or estimate. The second best is the SCF, followed by the quantile method and the moment method. The ML approach makes it easy for one to give large-sample confidence intervals for the parameters, thus making it the more preferred method.
If X1,X2, … ,Xn are i.i.d. stable samples, Nolan, Panorska and McCulloch (2001) defined the log-likelihood function as:
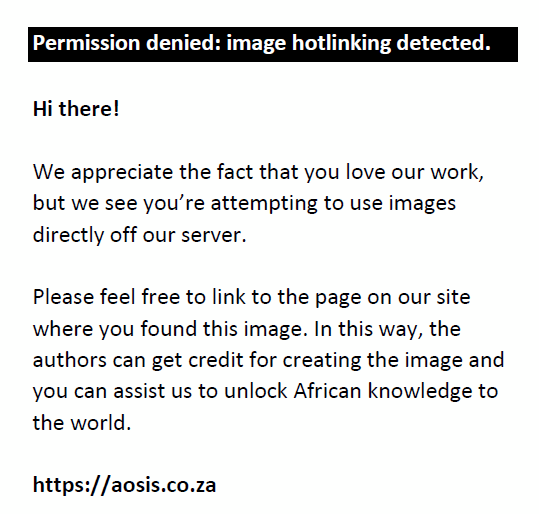
The lack of closed-form formulas for general stable densities is a major challenge in evaluating [Eqn 19]. It should be mentioned here that innovative ML estimation techniques employ two methods: the direct integration method (Nolan et al. 2001) and the fast Fourier transform (FFT) method for approximating the stable pdf (Mittnik et al. 1999). The two approaches can be evaluated based on the efficiency terms, while the types of approximation algorithms differentiate both. Nolan (2003) suggested a stable programme which establishes authentic computations of stable densities ranging between α > 0.1 and any β, γ and δ.
Value-at-risk and backtesting
Value-at-risk is a risk management tool that has become a benchmark for measuring market risks. This risk measure is used to evaluate the maximum possible loss for a portfolio over a given time period (McNeil, Frey & Embrechts 2005). In this article, we estimate VAR using the proposed distributions and compare them with the historical VAR values.
The VAR (for a given probability p) is defined as the pth quantile of F, that is,
where F−1 is the quantile function (Tsay 2013).
The strength of a model is the ability to forecast accurate VAR estimates for adequate capitalisation. In this article, we test VAR model identification and effectiveness by utilising the Kupiec LR unconditional coverage test (Kupiec 1995). The Kupiec likelihood test utilises the fact that a good model should have its proportion of violations of VAR estimates close to the corresponding tail probability, α (Chifurira & Chinhamu 2017; Chinhamu et al. 2014). The null hypothesis is that the expected proportion of violations is equal to α. Under this null hypothesis, the Kupiec statistic, which is given by:
is asymptotically distributed according to a chi-square distribution with one degree of freedom.
Our approach
The following steps are used for calculating VAR and then backtesting using the Kupiec LR test. An APARCH model is fitted to the return using the pseudo-ML procedure using a normal distribution governing the innovations.
- The standardised residuals are extracted from the model.
- The GPD (model 1), PIVD (model 2) and SD (model 3) are fitted to the standardised residuals using the ML estimation.
- The VAR is calculated for the three models.
Data
In this article, the data examined consist of the daily closing price of the All Share Index (ALSI) for the period 20 May 2005–31 May 2016 obtained from INET BFA. We divide the data into in-sample data set (20 May 2005–31 December 2013) and out-of-sample data set (02 January 2014–31 May 2016). The in-sample data are used for the model estimation and for forecasting risk, while the out-of-sample data are used for testing VAR forecast. As a result, the estimation window has 2155 observations, the testing window has 602 observations and thus the number of observations is 2757. We therefore obtain the daily log returns (rt) of the ALSI. The log returns are given by:
where Pt is the daily closing price of ALSI at time t and Pt−1 is the daily closing price of ALSI at time t−1. Figures 1a and b show the time series and log returns plots of the in-sample data, respectively.
The time series plot shows that the daily ALSI has a trend and hence is non-stationary in mean and variance. Using Figure 1b, the log returns seem to be stationary but the variance appears not to be constant over time indicating volatility clustering. To confirm the stationarity of the JSE ALSI log returns, the augmented Dickey–Fuller test is used to formally test for stationarity in mean and variance. The null hypothesis is that the log return series is non-stationary and the alternative hypothesis is that the log return series is stationary. The augmented Dickey–Fuller statistic is −13.612 with p-value of 0.01< 0.05; thus, rejecting the null hypothesis at 5% significance level means that the log returns are stationary. Table 1 presents the descriptive statistics for the daily JSE ALSI log returns.
 |
FIGURE 1: Time series plot of (a) daily JSE All Share Index and (b) daily JSE All Share Index log returns from 20 May 2005 to 31 December 2013 (in-sample data set). |
|
The mean returns are close to zero. The negative skewness is significantly different from zero and large excess kurtosis clearly illustrates the non-normality (asymmetric property of the log returns) of the distribution. As the p-value for Ljung–Box Q statistic is less than 0.05, we reject the null hypothesis of no presence of serial correlation. The p-value for the ARCH Lagrange multiple (ARCH-LM) statistic is less than 0.05. Thus, we reject the null hypothesis of the absence of potential time varying volatility (no arch effect) up to lag 20. These findings led to the adoption of an asymmetric ARCH (APARCH) model as discussed in Section 2.
Empirical results
This section presents the empirical evidence from the Financial Times Stock Exchange (FTSE) or JSE ALSI log returns data set. It examines the VAR performance of the APARCH (1,1) model combined with GPD, PTIVD and SDs.
Asymmetric generalised auto-regressive conditional heteroscedasticity type model fitting
In the first step, we fit the asymmetric GARCH-type models to the returns and check their adequacy because the returns have a significant skewness (asymmetric). The EGARCH (1,1), TGARCH (1,1) and APARCH (1,1) models are fitted to the FTSE or JSE ALSI log returns using the MLE method. Table 2 shows the ML parameter estimates and the standard errors in brackets of the asymmetric GARCH models with normal distribution innovation. The Akaike information criterion (AIC) and Bayesian information criterion (BIC) model selection criteria are also reported in Table 2.
| TABLE 2: Maximum likelihood parameter estimates of asymmetric generalised auto-regressive conditional heteroscedasticity models. |
In Table 2, it is observed that the ML parameters’ estimates for the three asymmetric GARCH models fitted to the FTSE or JSE ALSI log returns are significant at least at 10% level of significance. The APARCH (1,1) model has the lowest AIC and BIC values and is selected as the best asymmetric GARCH-type model. The APARCH (1,1) model has successively captured the volatility clustering with Ljung–Box p-value 0.3367 > 0.05 and ARCH-LM p-value 0.3743 > 0.05 of the extracted standardised residuals. The model is found to be able to capture the asymmetry of the returns with p-value 0.2862 > 0.05 of the sign bias statistic. Table 3 shows the descriptive statistics of the extracted standardised residuals.
| TABLE 3: Descriptive statistics of standardised residuals of the asymmetric power auto-regressive conditional heteroscedastic (1,1) model. |
The table reports summary statistics for the standardised residuals.
In Table 3, it is observed that the excess kurtosis value of the standardised residuals from the fitted APARCH (1,1) with normal distribution innovations is greater than zero. This indicates that there is still relatively more value in the tail. Therefore, the standardised residuals seem to have a tail heavier than that of normal distribution. To check for the non-normality of the standardised residuals, the Q–Q plot and Shapiro–Wilk tests are employed. Figure 2 shows the empirical density plot and a Q–Q plot of the standardised residuals.
 |
FIGURE 2: Q–Q plot of standardised residuals of asymmetric power auto-regressive conditional heteroscedastic (1,1) model with normal distribution. |
|
In Figure 2, the Q–Q plot suggests that the standardised residuals seem to diverge at the tails. This is confirmed by the Shapiro–Wilk test statistics with p-value 0.000 < 0.05. This confirms that the standardised residuals of APARCH (1,1) have a much heavier tail than that of the normal distribution, thus justifying using heavy-tailed distributions to model the extracted standardised residuals from APARCH model.
We fit the GPD, PTIVD and SDs to the standardised residuals from the APARCH model. Fitting a statistical distribution usually assumes that the data are i.i.d., that is, randomness, with no serial correlation and no heteroscedasticity. We tested for randomness using the Bartels’ rank test. The null hypothesis is that the standardised residuals are i.i.d. The p-value of the Bartels’ rank tests statistic is 0.9117 which is greater than 0.05, indicating that the standardised residuals are i.i.d. From Table 3, we noted that the standardised residuals are not serially correlated and have no heteroscedasticity.
Combining asymmetric power auto-regressive conditional heteroscedastic (1,1) with heavy-tailed distributions
Asymmetric power auto-regressive conditional heteroscedastic (1,1)–generalised Pareto distribution model
To fit the GPD model, we check whether the tails of the standardised residuals follow a Pareto distribution. Figure 3 shows the Pareto quantile plot for the extracted standardised residual.
 |
FIGURE 3: Pareto quantile plot of asymmetric power auto-regressive conditional heteroscedastic (1,1) model (normal innovations) residuals. |
|
In Figure 3, the tail of the data is almost a straight line, confirming that the standardised residuals may follow a GPD. The mean excess and the parameter stability plots were used to come up with a reasonable high threshold τ. Figure 4 shows the mean excess plot.
 |
FIGURE 4: Mean excess plot of asymmetric power auto-regressive conditional heteroscedastic (1,1) model (normal innovations) residuals. |
|
The suitable threshold must lie where there is a positive change in the mean excess. In Figure 4, the optimal threshold seems to lie around 2. The selection of the suitable threshold is performed empirically. We use the parameter stability plot to check the threshold where the parameters are most stable. Figure 5 shows the parameter stability plot for threshold between 1.5 and 2.5.
 |
FIGURE 5: Parameter stability plot of asymmetric power auto-regressive conditional heteroscedastic (1,1) model (normal innovations) residuals. |
|
Figure 5 shows that the estimated parameters are more stable when τ ≥ 1.7. The Pareto quantile plot is then used to obtain the optimal threshold of 1.7865. There are 635 observations above the threshold. As the exceedances above the threshold cannot be assumed to be i.i.d., declustering was performed.
We fit GPD (model 1) to the declustered exceedances. Table 4 reports the ML parameter estimates with standard errors in brackets.
| TABLE 4: Maximum likelihood estimates of the generalised Pareto distribution for the asymmetric power auto-regressive conditional heteroscedastic (1,1)–generalised Pareto distribution model. |
Figure 6 shows the diagnostic plots for the GPD model.
 |
FIGURE 6: Diagnostic plots for the asymmetric power auto-regressive conditional heteroscedastic (1,1)–generalised Pareto distribution model. (a) Probability plot, (b) quantile plot, (c) return-level plot and (d) density plot. |
|
The probability plot (top left panel) and the quantile plot (top right panel) suggest that the exceedances seem to follow the GPD model. The return-level plot (bottom left panel) confirms that the GPD model is adequate to estimate VAR of the exceedances. Finally, the density plot (bottom right panel) seems consistent with the histogram of the data. Thus, all the diagnostic plots suggest that the exceedances follow the GPD model. The diagnostic plots indicate that the GPD provides a good depiction of the residuals of an APARCH (1,1) model.
Asymmetric power auto-regressive conditional heteroscedastic (1,1)–Pearson type-IV distribution model
The PIVD is fitted to the standardised residuals extracted from the APARCH (1,1) model with normal innovations. The parameters are estimated using the method of ML. The ML procedure is carried out using R package (PearsonDS). Table 5 shows the ML estimates of the PIVD fitted to the standardised residuals of the APARCH (1,1) model with normal innovations.
| TABLE 5: Maximum likelihood estimates of the Pearson type-IV distribution for the asymmetric power auto-regressive conditional heteroscedastic (1,1)–Pearson type-IV distribution model. |
In Table 5, the value of  , thus satisfying the condition for a PIVD. The AD statistic is significant; thus, the PIVD is a good fit of the standardised residuals extracted from the APARCH (1,1) model.
Asymmetric power auto-regressive conditional heteroscedastic (1,1)–stable distribution model
The SD is also fitted to the extracted standardised residuals of the APARCH (1,1) model. The model is referred to as APARCH (1,1)–SD model. Table 6 shows the ML parameter estimates of an SD fitted to the standardised residuals of APARCH (1,1) model.
| TABLE 6: Maximum likelihood estimates of the stable distribution for the asymmetric power auto-regressive conditional heteroscedastic (1,1)–stable distribution model. |
In Table 6, the value of the index of stability ( ) is 1.9163 which is less than 2. This suggested that the tail of the standardised residuals follows a Pareto law, indicating that the distribution is heavy-tailed and also has infinite variance. The stable skewedness ( ) is −1, suggesting that the standardised residuals are skewed to the left. The AD statistics has a p-value of 0.3248 > 0.05, confirming that the SD is a good fit for the standardised residuals.
Value-at-risk is calculated for each model. Table 7 presents VAR estimates for the APARCH (1,1)–GPD, APARCH (1,1)–PIVD and APARCH (1,1)–SD models at different levels of significance. We note that the APARCH (1,1) with Student t-distribution governing the innovations produced high VAR estimates. This suggests that the APARCH (1,1)–Student t-distribution model is inadequate to fully capture the ‘stylised facts’ exhibited by the FTSE or JSE ALSI returns. This phenomenon is well known in the literature.
| TABLE 7: Value-at-risk estimates for the asymmetric power auto-regressive conditional heteroscedastic (1,1) model combined with different distributions. |
The models are backtested using Kupiec test. The p-values of the Kupiec test for both the in-sample data set and out-of-sample data set are summarised in Table 8.
| TABLE 8: Value-at-risk backtesting for Johannesburg Stock Exchange All Share Index returns. |
The VAR estimates from the APARCH (1,1)–Student t-distribution produced the lowest p-value less than 0.05 for the Kupiec LR test statistic at almost all VAR levels. The best model for VAR estimation for the JSE All Share Index returns differs at different VAR levels. The results show that the APARCH (1,1) with GPD innovations produced the highest and significant p-values at 97.5% and 95% levels. This indicates that the APARCH (1,1)–GPD model outperforms the APARCH (1,1) model with PIVD innovations and APARCH (1,1) model with SD innovations at 97.5% and 95% levels. Thus, at these levels, the most robust VAR model is APARCH (1,1)–GPD model. While at 90% VAR level, the APARCH (1,1) model with PIVD innovations produced the highest p-value. We also observe the same performance of the models in the out-of-sample data set. The APARCH (1,1)–SD model failed to adequately estimate VAR at 90% and 95% levels with p-value(s) < 0.05. In general, we conclude that the GPD and PIVD favourably capture the extreme risk in JSE All Share Index returns.
Conclusion
In this article, we examined the suitability of using APARCH (1, 1) framework combined with heavy-tailed distributions for modelling VAR for JSE All Share Index returns. The APARCH framework was used to capture volatility and asymmetric characteristics exhibited by financial returns, while the heavy-tailed distributions are used to capture the heavy-tailedness of actual return distributions. The GPD, PIVD and the SDs are applied to the i.i.d. standardised residuals from the APARCH (1,1) model with normal innovations and VAR is calculated at different levels. Adequacy of the resulting VAR estimates was tested using the Kupiec LR test. Backtesting using the Kupiec LR test has shown that the APARCH (1,1) with GPD governing the innovations is the most robust model at 97.5% and 95% level. At 90% level, the APARCH (1,1) with PIVD governing the innovations is the most robust model for estimating VAR for FTSE or JSE ASPI returns. The backtesting procedure emphasised the superiority of the GPD and PIVD models over Student-t and stable models, thus providing a very good candidate as an alternative distributional scheme.
Acknowledgement
The authors are grateful to Prof. M. Murray at the University of KwaZulu-Natal for editing the manuscript.
Competing interests
The authors declare that they have no financial or personal relationships that may have inappropriately influenced them in writing this article.
Authors’ contributions
R.C. contributed to the introduction, methodology, data analysis, results, discussion and conclusion. K.C. contributed to the literature review, discussion, recommendations of the study and editing of the manuscript.
Ethical considerations
This article followed all ethical standards for research without direct contact with human or animal subjects.
Funding
This research received no specific grant from any funding agency in the public, commercial or not-for-profit sectors.
Data availaibility statement
Data sharing is not applicable to this article as no new data were created or analysed in this study.
Disclaimer
The views and opinions expressed in this article are those of the authors and do not necessarily reflect the official policy or position of any affiliated agency of the authors.
References
Bhattacharyya, M., Chaudhary, A. & Yadav, G., 2008, ‘Conditional VaR estimation using Pearson’s type IV distribution’, European Journal of Operational Research 191(2), 386–397. https://doi.org/10.1016/j.ejor.2007.07.021
Baillie, R.T., Bollerslev, T. & Mikkelsen, H.O., 1996, ‘Fractionally integrated generalized autoregressive conditional heteroscedasticity’, Journal of Econometrics 74(1), 3–30. https://doi.org/10.1016/S0304-4076(95)01749-6
Beirlant, J., Goegebeur, Y., Segers, J. & Teugels, J., 2004, Statistics of extremes: Theory and applications, Wiley Series in Probability and Statistics, New York.
Bollerslev, T., 1986, ‘Generalized autoregressive conditional heteroskedasticity’, Journal of Econometrics 31(3), 307–327. https://doi.org/10.1016/0304-4076(86)90063-1
Bollerslev, T., 1987, ‘A conditional heteroskedastic time series model for speculative prices and rates of return’, The Review of Economics and Statistics 69(3), 542–547. https://doi.org/10.2307/1925546
Bollerslev, T. & Mikkelsen, H.O., 1996, ‘Modelling and pricing long-memory in stock market volatility’ Journal of Econometrics 73(1), 151–184. https://doi.org/10.1016/0304-4076(95)01736-4
Chan, K.F. & Gray, P., 2006, ‘Using extreme value theory to measure value-at-risk for daily electricity spot prices’, International Journal of Forecasting 22(2), 283–300. https://doi.org/10.1016/j.ijforecast.2005.10.002
Cheng, R., 2011, ‘Using Pearson type IV and other cinderella distributions in simulation’, Proceedings of the 2011 Winter Simulation Conference, University of Southampton, pp. 457–468, Institute of Electrical and Electronics Engineers (IEEE), Phoenix, USA.
Chifurira, R. & Chinhamu, K., 2017, ‘Using the generalized Pareto and Pearson type-iv distributions to measure value-at-risk for the daily South African mining index’, Studies in Economics and Econometrics 41(1), 33–54.
Chinhamu, K., Huang, C.K., Huang, C.S. & Hammujuddy, J., 2014, ‘Empirical analyses of extreme value models for the South African mining index’, South African Journal of Economics 83(1), 41–55. https://doi.org/10.1111/saje.12051
Coles, S., 2001, An introduction to statistical modelling of extreme values, Springer Series in Statistics, Springer-Verlag, London.
Davidson, J., 2004, ‘Moment and memory properties of linear conditional heteroscedasticitymodels, and a new model’, Journal of Business and Economic Statistics 22(1), 16–29. https://doi.org/10.1198/073500103288619359
Ding, Z., Granger, C.W.J. & Engle, R.F., 1993, ‘A long memory property of stock market returns and a new model’, Journal of Empirical Finance 1(1), 83–106. https://doi.org/10.1016/0927-5398(93)90006-D
Dumouchel, W.H., 1973, ‘Stable distributions in statistical inference. 1:Symmetric stable distributions compared to other symmetric long-tailed distributions’, JASA 68(342), 469–477. https://doi.org/10.1080/01621459.1973.10482458
Embrechts, P., Klüppelberg, C. & Mikosch, T., 2013, Modelling extremal events: for insurance and finance, vol. 33, Springer Science & Business Media, New York.
Engle, R.F., 1982, ‘Autoregressive conditional heteroskedasticity with estimates of the variance of United Kingdom inflation’, Econometrica 50(4), 987–1007. https://doi.org/10.2307/1912773
Engle, R.F. & Bollerslev, T., 1986, ‘Modelling the persistence of conditional variances’, Econometric Reviews 5(1), 1–50. https://doi.org/10.1080/07474938608800095
Fama, E.F., 1965, ‘The behavior of stock-market prices’, Journal of Business 38(1), 34–105. https://doi.org/10.1086/294743
Glosten, L.R., Jagannathan, R. & Runkle, D.E., 1993, ‘On the relation between the expected value and the volatility of the nominal excess return on stocks’, The Journal of Finance 48(5), 1779–1801. https://doi.org/10.1111/j.1540-6261.1993.tb05128.x
Hassan, S., 2013, South African capital markets: An overview, Working Paper No. 13/04, South African Reserve Bank, Pretoria.
Johnson, N.L., Kotz, S. & Balakrishman, N., 1994, Continuous univariate distributions, vol. 1, 2nd edn., John Wiley & Sons, Hoboken, NJ.
Karlsson, L., 2002, ‘GARCH modelling: Theoretical survey, model implementation and robustness analysis’, Unpublished master’s thesis, Kungl Tekniska Högskolan.
Kogon, S.M. & Williams, D.B., 1998, ‘Characteristic function based estimation of stable parameters’, in R. Adler, R. Feldman & M. Taqqu (eds.), A practical guide to heavy tailed data, pp. 311–338, Birkh¨auser, Boston, MA.
Kupiec, P., 1995, ‘Techniques for verifying the accuracy of risk management models’, Journal of Derivatives 3(2), 73–84. https://doi.org/10.3905/jod.1995.407942
Ma, X. & Nikias, C.L., 1995, ‘Parameter estimation and blind channel identification in impulsive signal environments’, IEEE Transactions on Signal Processing 43(12), 2884–2897. https://doi.org/10.1109/78.476432
Makhwiting, M.R., 2014, ‘Modelling volatility and financial market risks of shares on the Johannesburg stock exchange’, Master of Science, University of Limpopo.
Mandelbrot, B., 1963, ‘The variation of certain speculative prices’, Journal of Business 36(4), 394–419. https://doi.org/10.1086/294632
McCulloch, J.H., 1986, ‘Simple consistent estimators of stable distribution parameters’, Communication in Statistics- Simulation and Computations 15(4), 1109–1136. https://doi.org/10.1080/03610918608812563
McNeil, A., Frey, R. & Embrechts, P., 2005, Quantitative risk management: Concepts, techniques, and tools’, Princeton University Press, Princeton, NJ.
Mittnik, S., Rachev, S.T., Doganoglu, T. & Chenyao, D., 1999, ‘Maximum likelihood estimation of stable Paretian models’, Mathematical and Computer Modelling 29(10–12), 275–293. https://doi.org/10.1016/S0895-7177(99)00110-7
Nagahara, Y., 1999, ‘The PDF and CF of Pearson type IV distribution and the ML estimation of the parameters’, Statistics and Probability Letters 43(3), 251–264. https://doi.org/10.1016/S0167-7152(98)00265-X
Nelson, D.B., 1991, ‘Conditional heteroskedasticity in asset returns: A new approach’, Econometrica 59(2), 347–370. https://doi.org/10.2307/2938260
Nolan, J.P., 2014, ‘Final modeling with heavy-tailed stable distributions’, Wiley Interdisciplinary Reviews: Computational Statistics 6(1), 45–55. https://doi.org/10.1002/wics.1286
Nolan, J.P., Panorska, A.K. & McCulloch, J.H., 2001, ‘Estimation of stable spectral measures’, Mathematical and Computer Modelling 34(9–11), 1113–1122. https://doi.org/10.1016/S0895-7177(01)00119-4
Nolan, J.P., 2003, ‘Modeling financial data with stable distributions’, in S.T. Rachev (ed.), Handbook of heavy tailed distributions in finance: Handbooks in finance, pp. 104–130, Elsevier Science, Netherlands.
Ojeda, D., 2011, ‘Comparative study of stable parameter estimators and regression with stably distributed errors’, PhD Thesis, American University, ProQuest Dissertations Publishing, Washington, DC.
Paolella, M.S., 2016, ‘Stable-GARCH models for financial returns: Fast estimation and tests for stability’, Econometrics 4(25), 1–28. https://doi.org/10.3390/econometrics4020025
Ren, F. & Giles, D., 2007, Extreme value analysis of daily Canadian crude oil, Econometrics Working Paper EWP0708, Department of Economics, University of Victoria, Victoria, Canada, ISSN: 1485-6441.
Shabani, M., Gharneh, N.S. & Esfahanipour, A., 2017, ‘Comparing the performance of GARCH (p, q) models with different methods of estimation for forecasting crude oil market volatility’, Journal of Industrial and Systems Engineering 9(4), 80–92.
Stavroyiannis, S., Makris, I., Nikolaidis, V. & Zarangas, L., 2012, ‘Econometric modeling and value-at-risk using the Pearson type-IV distribution’, International Review of Financial Analysis, 22 (April), 10–17. https://doi.org/10.1016/j.irfa.2012.02.003
Tsay, R.S., 2013, An introduction to analysis of financial data with R, Wiley & Sons, Hoboken, NJ.
Tse, Y.K., 1998, ‘The conditional heteroskedasticity of the yen–dollar exchange rate’, Journal of Applied Econometrics 193(1), 49–55. https://doi.org/10.1002/(SICI)1099-1255(199801/02)13:1%3C49::AID-JAE459%3E3.3.CO;2-F
|
Email this article 
Hide
Show all
