Abstract
Orientation: The literature on exchange rate pass-through appears to have shifted from the question of whether the pass-through is complete or incomplete to whether or not it is sufficient to assume that the pass-through is exogenous despite the vulnerability of exchange rates to shocks because of other external prices.
Research purpose: The primary objective of this study is to examine the role of oil prices in the dynamics of exchange rate pass-through to domestic inflation in net oil-exporting and oil-importing countries.
Motivation for the study: Motivated by the increasing evidence of significant responses of exchange rates to changes in oil prices, this study hypothesises that changes in oil prices matter for the degree and direction of exchange rate pass-through in the context of oil-importing and oil-exporting dichotomy. This study attempts to re-define the areas of ambiguities on the exchange rate, and other accompanying factors linked to it for clarity.
Research approach/design and method: Using a macro panel data set, we explore the newly formulated non-linear panel autoregressive distributed lag model to account for asymmetries in our assessment of the role of oil prices in the degree and direction of pass-through of the exchange rate. Thus, in addition to reflecting the pass-through in a nonlinear form, this study also accounts for heterogeneity as well as non-stationarity. Besides, we also evaluate the role of prices in the pass-through of exchange rates symmetrically using the symmetric version of the Panel ARDL model.
Main findings: Given the data under consideration, our empirical findings give credence to the school of thought challenging the widely held assertion that the declining pass-through of the exchange rate is mainly caused by the phenomenon of the developed market.
Practical/managerial implications: We also find that accounting for asymmetries in the pass-through matters for the extent to which changes in oil prices accelerate the degree of pass-through.
Contribution/value-add: This study finds evidence of an insignificant role of oil prices in the pass-through of the exchange rate fluctuations to inflation. Once the pass-through is captured asymmetrically, it becomes evident that changes in oil prices matter in the pass-through.
Keywords: oil price; exchange rate; net oil-importers and exporters; panel ARDL; exchange rate pass-through (ERPT) fluctuations.
Introduction
Whilst price stability remains the primary objective of monetary authorities in nearly all countries, the task of achieving low inflation is challenging partially because of the vulnerability of domestic prices to factors that are beyond the control of monetary policy. Prominent amongst these is the exchange rate pass-through (ERPT) fluctuations. Being the value of a country’s currency for international trade in goods and services, the exchange rate is arguably the most important price in an open economy and thus has both direct and indirect effects on other macroeconomic fundamentals, namely imports, exports, external reserves, interest rates and inflation. More importantly, fluctuations in exchange rates may be transmitted into domestic inflation through increase in import prices of final goods (direct channel) and prices of imported intermediate inputs (indirect channel).
The transmission mechanism through which a change in domestic prices (import and consumer prices) takes place is because of changes in exchange rate movements and is known as ‘exchange rate pass-through’. Thus, the ability of central banks to mitigate the pass-through effect of exchange rate fluctuations depends, amongst others, on the proper evaluation of the extent and timing of ERPT. For many years, research has been carried out on the transmission of exchange rate movements into domestic prices with different methods of analyses yielding different results (see, e.g., Barhoumi 2006; Brun-Aguerre, Fuertes & Phylaktis 2012; Choudhria & Hakura 2006, 2014; Donayre & Panovska 2016; Ghosh 2013; Jiang & Kim 2013; Jimborean 2013; Karagoz, Demirel & Bozdag 2016; Marazzi & Sheets 2007; Mirdala 2014; Mohammed et al. 2015; Uddin, Quaosar & Nandi 2014).
Notwithstanding the large number of empirical studies on the ERPT, several extant studies have continued to ignore some key insights in their methodological approaches and empirical evaluation of ERPT. Firstly, the extent to which changes in exchange rates accelerate or slow down domestic inflation cannot be investigated in isolation of underlying shocks that cause fluctuations in exchange rate movements. Secondly, there has been an ongoing debate on whether the symmetric or asymmetric nature of changes in exchange rate matters for the degree, timing and direction of its pass-through. The non-consideration for shocks and asymmetric characteristics of exchange rates tends not only to introduce biases in the measure of ERPT but also to undermine the efficiency of monetary authorities in predicting the future inflation. To bridge this gap, this study is built on the increasing evidence of a significant impact of changes in oil prices on exchange rates (see Ahmad & Hernandez 2013; Aloui, Aïssa & Nguyen 2013; Atems, Kapper & Lam 2015; Bal & Rath 2015; Bouoiyour et al. 2015; Chen et al. 2016; Chou & Tseng 2015; Fowowe 2014; Jiang & Gu 2016; Le & Chang 2011; Park & Ratti 2008; Reberodo 2012; Turhan et al. 2014; Yang, Cai & Hamori2017) to control for the role of oil prices in an investigation of ERPT fluctuations to domestic prices within the context of oil-export and oil-import economies.
Unlike a number of extant studies that have used oil prices to merely control for supply shocks of inflation, the inclusion of oil prices in the context of this article is to capture the responsiveness of exchange rates to other external price shocks. To the best of our knowledge, this study is the first to have proposed to investigate whether the role of oil prices in ERPT is sensitive to the operating economic environment. This is the motivation for our choice of the case study, namely net oil-exporting and oil-importing economies. Whilst acknowledging that there are more than 20 and up to 15 countries ranked amongst the top oil-importing and oil-exporting countries, respectively (see CIA-World Factbook, 2018- Oil Production for details on the ranking), the choice of the selected countries was mainly informed by the availability of data. We further account for the non-linearity of the exchange rate movements using Salisu and Isah’s (2017) newly proposed non-linear panel autoregressive distributed lag (NARDL). The essence is to determine the extent to which asymmetries matter for the role of oil prices in the pass-through.
The rest of this article is structured as follows: Section 2 presents the model specification on ERPT; Section 3 discusses the data and conducts some preliminary analyses and Section 4 is an outline of econometric methods and estimation procedures used in the study. Section 5 presents the findings, whilst conclusions and policy recommendations are presented in Section 6.
The model
The basic approach to estimate ERPT, particularly at the macroeconomic level, has been to regress changes in some measure of domestic prices on past and present changes in exchange rates and additional control variables. Following Campa and Goldberg (2005), Burstein and Gopinath (2014) and Cheikh and Rault (2015), our baseline model is given by (where all the variables are expressed in log form):
where  is the domestic currency import price, eit is the exchange rate, is the domestic currency import price, eit is the exchange rate,  denotes export costs and xit is the vector of variables that includes demand condition and competitor prices in the importing country, amongst other control variables. The term ɛit is a white noise error term, subscript ‘i’ the country index and ‘t’ is the time counter. One weakness of the pass-through model in Equation 1, as pointed out by Barhoumi (2006), is that the pass-through of exchange rates (eit) and export costs denotes export costs and xit is the vector of variables that includes demand condition and competitor prices in the importing country, amongst other control variables. The term ɛit is a white noise error term, subscript ‘i’ the country index and ‘t’ is the time counter. One weakness of the pass-through model in Equation 1, as pointed out by Barhoumi (2006), is that the pass-through of exchange rates (eit) and export costs  into import prices into import prices  are the same; hence, there is a tendency of biases in the estimate of the pass-through coefficient if the costs or markup proxies are correlated with exchange rates (see Campa & Goldberg 2002). are the same; hence, there is a tendency of biases in the estimate of the pass-through coefficient if the costs or markup proxies are correlated with exchange rates (see Campa & Goldberg 2002).
Notwithstanding the foregoing discussion, Athukorola and Menon (1995) have provided economic reasons to justify that such coefficient restrictions may not hold, particularly given the likely incompatibility of price proxies attributable to differences in aggregation levels and methods of data collection. Further justifying why such restrictions may not hold is the argument put forth by Bache (2002) that exchange rates are more variable than costs, and a reasonable conjecture is that exporters will be more willing to absorb into their markup changes in exchange rates than changes in the costs, which are likely to be permanent. It is in this light, therefore, that this study is proposing to relax such restriction and employ Equation 2 as its baseline empirical model for evaluation of ERPT fluctuations to domestic prices:
Whilst all the variables remain as defined previously, the term xit, which is a vector of control variables in Equation 1, has now been expanded to reflect the demand condition, competitor prices and changes in world oil prices. Oil prices are included in our pass-through model specification to reflect the peculiarity of the investigated economies (net oil-exporting and oil-importing countries) and to examine whether changes in oil prices influence the degree of pass-through. In addition, it is clear that changes in exchange rate also influence import prices indirectly through their effects on commodity prices. Thus, taking this as a transmission channel further justifies our inclusion of oil prices as an additional control variable in the pass-through specification.
A number of extant studies have assumed that exchange rates are exogenous in their pass-through specification. To this end, they often neglect the underlying shocks that cause exchange rate fluctuations in the first place, which could lead to biased and inconsistent estimates of the pass-through results. To bridge this gap, we further propose an extension to the baseline pass-through model specification in Equation 2 to include an interaction term denoting the responsiveness of exchange rate to changes in oil prices:
Our primary concern in this study is the pass-through elasticity corresponding to the coefficients of exchange rates variables, namely β1 and β6, in the baseline and extended models, respectively. If β1 < β6 then the responsiveness of exchange rates to changes in oil prices is likely to accelerate the degree of ERPT to domestic prices and the reverse is likely to be the case if β1 > β6
There is considerable debate in literature on whether ERPT fluctuation to domestic prices is linear (symmetric) or non-linear (asymmetric). Therefore, we further present the exchange rate (e) in Equation 2 in a non-linear formulation (see Equation 4) to capture the probable asymmetric effect of the pass-through:
Equation 4 is a non-linear (asymmetric) version of the baseline model with the exchange rate decomposed into negative (depreciation) and positive (appreciation) values. Whilst this has been a standard approach for capturing asymmetries in the specification of ERPT, the novelty of our study in this context centred on whether such asymmetries matter for the role of oil price as a potential accelerator of the degree of pass-through. To achieve this, we again relax the exogenous assumption of the standard non-linear (asymmetric) pass-through specification in Equation 4 to capture the probable non-linear responses of exchange rate to oil price shocks (see Equation 5):
Thus, the extended interaction term  in Equation 5 not only captures the asymmetric pass-through but also accounts for the probable role of oil price shocks as a source of fluctuations in the movement of exchange rates. in Equation 5 not only captures the asymmetric pass-through but also accounts for the probable role of oil price shocks as a source of fluctuations in the movement of exchange rates.
Data and preliminary analysis
Data source and measurement
Data for all variables used in this study are sourced from the International Monetary Fund’s (IMF) International Financial Statistics (IFS) and the Organisation of Economic Co-operation and Development (OECD) online database. The data cover the period from the first quarter of 1990 to the third quarter of 2017. The dependent variable, import domestic prices (pm), is calculated as the log of import price index. Amongst the independent variables, the exchange rate is measured as the log of the nominal effective exchange rate calculated as the trade-weighted average of respective countries’ exchange rates against other currencies. The appropriateness of this measure (as opposed to the bilateral exchange rate) for capturing the pass-through of the exchange rate (e) hinges on the fact that countries often engage in trade with more than one country.
With regard to the foreign export costs variable, the marginal costs of foreign producers are often difficult to measure primarily because they are not directly observable. Therefore, this study employs a measure used by Campa and Goldberg (2005) and Bailliu and Fujii (2004), which is calculated as follows:
where Eit is the nominal effective exchange rate,  is the wholesale price index (because of data unavailability for some countries, we use the All Prices Composite Consumer Price Index) and Qit is the real effective exchange rate. Taking the logarithm of each variable, we obtain the following expression: is the wholesale price index (because of data unavailability for some countries, we use the All Prices Composite Consumer Price Index) and Qit is the real effective exchange rate. Taking the logarithm of each variable, we obtain the following expression:  . .
We use the log of industrial production index to measure the demand condition (y). Following Olivei (2002) and Bussie`re (2013), domestic competitors’ prices (cp) are measured as the log of Producer Price Index (PPI), whilst the log of Brent international crude oil prices is used as a proxy for changes in oil prices. Finally, the choice of the selected major oil-importing (Belgium, Germany, Italy, Japan, the Netherlands, Spain, UK and USA) and oil-exporting (Algeria, Canada, Nigeria, Norway and Russia) countries is informed by the availability of data.
Preliminary analysis
As a pretest condition for dealing with panel data with a large time series (T) dimension, we subject each of the variables under consideration to a stationarity test. The first category of panel unit root tests involves testing the null hypothesis of (panel) unit roots with a common process (Breitung 2000; Harris & Tzavalis 1999; Levin, Lin & Chu 2002 tests). The second category, including Im, Pesaran and Shin (2003) and Maddala and Wu (1999), assumes unit roots with individual unit root process, whilst the third category also assumes unit roots in the null hypothesis but in the presence of cross-sectional dependence (Pesaran 2007). The fourth category, however, tests the null hypothesis of no unit roots with common unit root processes (Hadri 2000, Lagrange multiplier test). Based on their hypotheses and test regressions, these tests have been categorised into stationary (the fourth type) and non-stationary (first, second and third type) tests in literature. Besides, the Pesaran (2007) unit root test is particularly important for this study as it could also be used to test whether the various cross-sections in each group are homogenous or heterogeneous. The null hypothesis for the test assumes homogeneous non-stationary series as opposed to the alternative hypothesis of possible heterogeneous alternatives.
We start with two main variables of interest, namely import prices and exchange rates. The unit root test results indicate that import price indexes are integrated of order one [I(1)] across the two economies with the only exception being the Levin et al. (2002) test in the case of oil-importing economies and the Hadri (2000) test in the case of net oil-exporting economies. Similarly, the Pesaran (2007) test results indicate that the import prices are heterogenous stationary of order one [I(1)] for the net oil-exporting group and stationary for the net oil-importing group. However, the cross-sections seem to be heterogenous irrespective of the economy group under consideration. The unit root test results for exchange rates are largely mixed, except for the Pesaran (2007) test, whose results consistently predict exchange rates as heterogenous stationary irrespective of the economy group under consideration. For other macro-economic factors included in ERPT specifications, the unit root test results as documented in Table 1 (Panel A and Panel B) show that they are either I(0) or I(1), thus validating the choice of the panel-ARDL model as the preferred estimation framework in the context of this study.
Econometric method and estimation procedures
Several studies have attempted to estimate pass-through elasticities as specified in Equations 2 and 3 in first differences (see, e.g., Bailliu & Eiji 2004; Campa & Goldberg 2004; Campa & Gonzàlez 2006). This type of specification allows for the estimation of short-run and long-run ERPT. Our empirical approach, however, requires that we use a technique that is suitable for dynamic panel data, and the essence is to take into consideration the stationarity of the variables and their co-integration relationship. As a consequence, this article explores the mean-group (MG) and pooled mean-group (PMG) estimators for its non-stationary dynamic panels in which the parameters are assumed heterogeneous across groups to estimate symmetric ERPT fluctuations to domestic prices in the net oil-exporting and oil-importing economies.
The suitability of this technique for modelling panel data with a large cross-section dimension (numbers of countries, in our case [N]) and a large T dimension makes it the most appropriate one in the context of this study. As pointed out by Blackburne and Frank (2007), the asymptotics of large N and large T dynamic panels are different from the asymptotics of traditional large N and small T dynamic panels. For example, estimators for small T panel estimation such as fixed-effect and random-effect estimators and generalised method-of-moments estimators usually require pooling individual groups and allowing only the intercepts to differ across the groups with the slope coefficients assumed to be homogenous. Pesaran, Shin and Smith (1997, 1999), however, have demonstrated that the assumption of homogeneity of slope parameters is often inappropriate when dealing with large N and large T. Besides, more worrisome is the fact that ignoring the slope parameter heterogeneity when in fact it exists may produce inconsistent and potentially misleading results.
Thus, the MG estimator of Pesaran and Smith (1995) and the PMG estimator of Pesaran et al. (1997, 1999) have been developed to capture any inherent slope heterogeneity in the panel data model and any potential bias that may result from using traditional methods. Essentially, the MG involves estimating N time-series regressions and averaging the coefficients, whereas the PMG estimator requires a combination of pooling and averaging of coefficients (see Pesaran & Smith 1995; Pesaran et al. 1997, 1999 for details the computational procedures). We begin our analysis by assuming a linear (symmetric) exchange pass-through to be estimated via the following panel-ARDL framework:
where  denotes the domestic prices of the log import price index for each country or unit ‘i’ over time ‘t’; eit is the log of nominal effective exchange rate for each country over time; and xit is the vector of other explanatory variables that include foreign export costs denotes the domestic prices of the log import price index for each country or unit ‘i’ over time ‘t’; eit is the log of nominal effective exchange rate for each country over time; and xit is the vector of other explanatory variables that include foreign export costs  , demand condition (yit), competitor prices (cpit), and the interaction term (eit, opit) reflecting the probable endogeneity effect of exchange rates. The term µi represents the group-specific effect and ‘i’ is the sampled units, whilst ‘t’ is the number of periods. For each cross-section, the long-run slope (elasticity) coefficient for ERPT is computed as , demand condition (yit), competitor prices (cpit), and the interaction term (eit, opit) reflecting the probable endogeneity effect of exchange rates. The term µi represents the group-specific effect and ‘i’ is the sampled units, whilst ‘t’ is the number of periods. For each cross-section, the long-run slope (elasticity) coefficient for ERPT is computed as 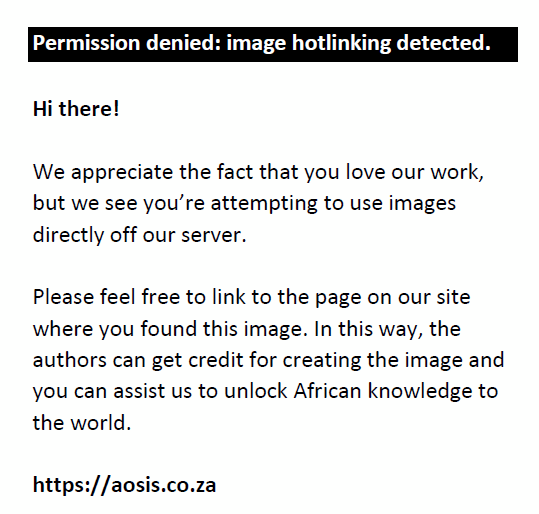 . However, because in the long run it is assumed that . However, because in the long run it is assumed that 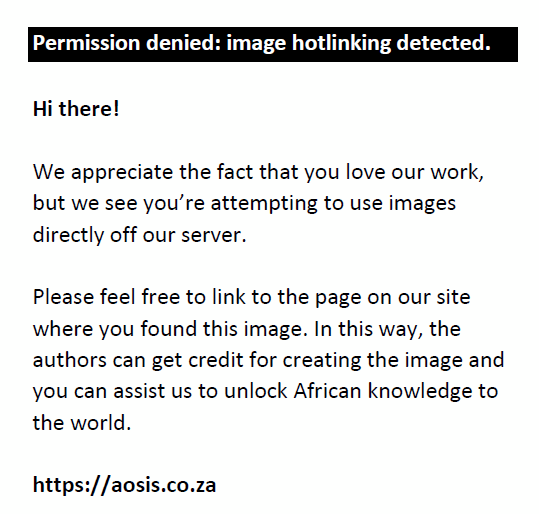 and Δet−j = 0, the elasticity for the short-run pass-through is expressed as.γij Therefore, Equation 6 can be re-specified to include an error correction term as follows: and Δet−j = 0, the elasticity for the short-run pass-through is expressed as.γij Therefore, Equation 6 can be re-specified to include an error correction term as follows:
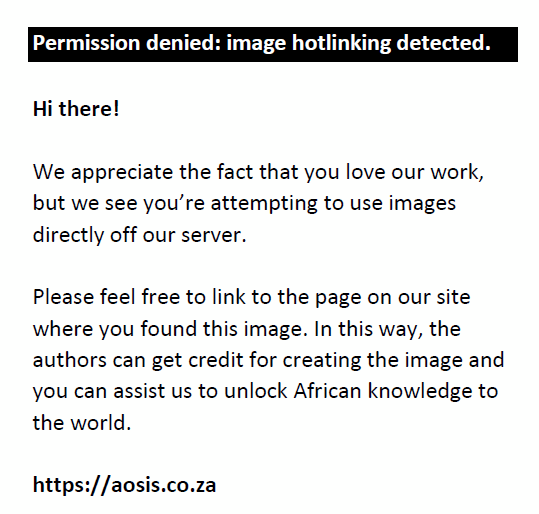
where 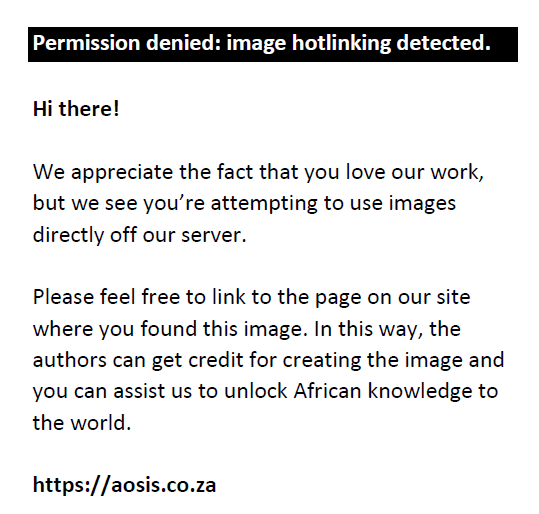 is the linear error correction term for each unit, and the parameter ψi is the error-correcting speed of adjustment term for each unit, which is also equivalent to. β1i Parameters φ0i, φ1i and φ2i are calculated as is the linear error correction term for each unit, and the parameter ψi is the error-correcting speed of adjustment term for each unit, which is also equivalent to. β1i Parameters φ0i, φ1i and φ2i are calculated as  , respectively. , respectively.
Although our primary concern is to determine the elasticity of ERPT, the approach for obtaining it as demonstrated above is the same for other explanatory variables in the various pass-through models specified. Thus, it is instructive that we explore a similar procedure to equally determine the slope coefficient of the interaction term to ascertain whether the responsiveness of exchange rates to changes in oil prices matters for the degree of pass-through.
Following the foregoing discussion, the MG estimator ensures that the intercepts, slope coefficients and error variances are allowed to differ across groups. Difference between the MG estimator and the PMG estimator lies in the way the long-run coefficients are treated. Unlike the MG estimator, the PMG estimator constrains the long-run coefficients to be equal across groups (as in the case of Fixed Effect estimator), although the intermediate estimator still allows the intercept, short-run coefficients and error variances to differ across the groups (as in the case of MG estimator). To determine the most appropriate and efficient approach, the Hausman test is usually employed. We postulate under the null hypothesis of this experiment that the PMG estimator is more efficient than the MG estimator. Therefore, non-rejection of null hypothesis implies the adoption of PMG estimator, whilst rejection indicates the adoption of MG estimator.
The non-linear (asymmetric) approach to exchange rate pass-through
Equations 6 and 7 show that there is no decomposition of exchange rates into positive (appreciation) and negative (depreciation) changes which effectively presumes a symmetric ERPT to domestic prices. In this section, we relax this symmetric assumption to enable us accommodate a probable asymmetric ERPT, where positive (appreciation) and negative (depreciation) changes of exchange rates are not expected to have an identical degree of pass-through to domestic inflation. Thus, we adopt a non-linear panel data representation of the Shin et al. (2014) model, the asymmetric version of Equation 6, which is given by:

where  and and  denote the positive (exchange rate appreciation) and negative (exchange rate depreciation) changes respectively. The long-run (elasticities) coefficients for the pass-through because of positive and negative exchange rate fluctuations (i.e. denote the positive (exchange rate appreciation) and negative (exchange rate depreciation) changes respectively. The long-run (elasticities) coefficients for the pass-through because of positive and negative exchange rate fluctuations (i.e.  and and  ) are calculated as ) are calculated as  respectively. This non-linear ERPT is computed as positive and negative partial sum decomposition of exchange rate fluctuations as defined below: respectively. This non-linear ERPT is computed as positive and negative partial sum decomposition of exchange rate fluctuations as defined below:
Again, the aforementioned procedure for computing a long-run (elasticity) coefficient for the asymmetric pass-through is also observed when the exchange rate is endogenously represented by interacting each of the decomposed exchange rate fluctuations with changes in oil prices. Similar to the symmetric pass-through modelling approach, the error correction version of Equation 8 is represented as follows:
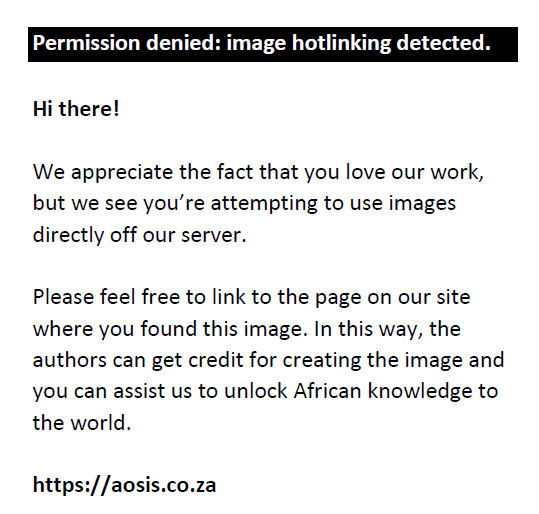
The error correction term (ξi,t-1) in Equation 9 captures the long-run equilibrium in the asymmetric panel ARDL specification, whilst its associated parameter (τi) is the speed of adjustment that measures how long the system would take to revert to its long-run equilibrium in the presence of a shock.
To refute or validate the significance of asymmetric pass-through effects of exchange rate fluctuations on the inflation rates of the investigated economies, the Wald restriction test is considered. Depending on the preferred estimator, the null hypothesis of no asymmetry, for instance, 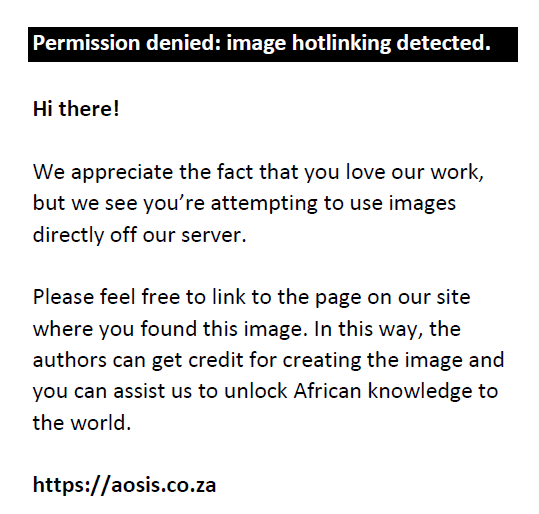 , is tested against the alternative , is tested against the alternative 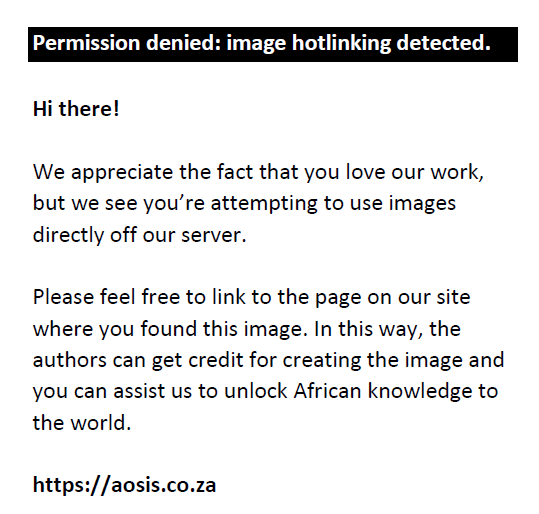 to establish the long-run asymmetric co-integration. On the other hand, the short-run asymmetric co-integration is tested with, to establish the long-run asymmetric co-integration. On the other hand, the short-run asymmetric co-integration is tested with, 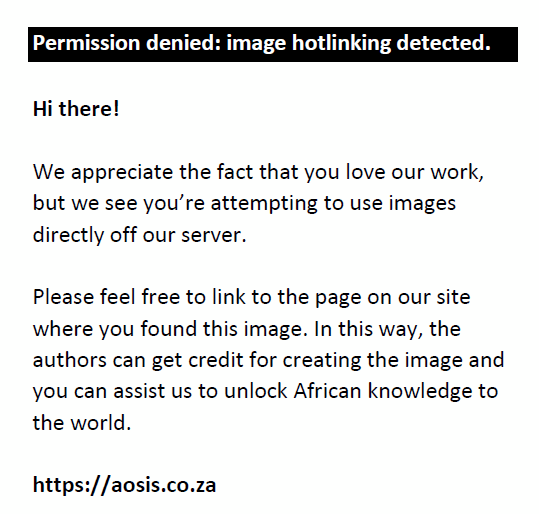 whilst the alternative hypothesis is stated as. whilst the alternative hypothesis is stated as.  . .
Ethical consideration
Ethical clearance and approval was obtained from the Humanities Social Sciences Research Ethical Committee of the University of KwaZulu-Natal on 12 July 2018, reference number HSS/0928/018D.
Empirical results and discussion
Results from the baseline exchange rate pass-through model
Starting with the baseline or traditional approach to modelling ERPT, the estimation results from the ERPT model specified in Equation 6 are summarised in Table 2. Starting with the Hausman test results, the table shows that the null hypothesis cannot be rejected, suggesting that PMG is the more efficient estimator for the estimation of specified ERPT model. The estimation results, in particular, show that the coefficients of the key variable of interest (i.e. changes in the exchange rate [Δeit]) are statistically significant, but the level of significance and the degree of the pass-through varies for the short run and long run across the two different economic groups under consideration. For instance, the estimated ERPT coefficients as reported in Table 2 show that the long-run ERPT elasticities are significant in both the net oil-importing and oil-exporting nations and bounded between 0.30% for the former and 0.22% for the latter. In the short-run, however, not only is the degree of ERPT at 0.17% and 0.13% for the respective economic groups relatively lower compared to the long-run ERPT, the significance of the pass-through is equally weak and is particularly evident in the oil-exporting economies.
| TABLE 2: Exchange rate pass-through panel regression results (symmetric model without interaction term). |
Although the pass-through seems incomplete irrespective of the short-run or long-run dynamics of the response of import prices to changes in exchange rates, the long-run coefficient of ERPT is relatively larger compared to the short-run coefficient. This may not be unconnected to the lagged adjustment of import prices to changes in exchange rates. We also find that whilst the degree of the pass-through is not significantly different across the two economies, it is relatively higher for the net oil-importing economies than for the net oil-exporting economies. Similarly, consistent with previous studies, we find that except for the domestic demand condition, particularly in the net oil-exporting economies, nearly all the macroeconomic variables in the ERPT model (e.g. foreign factor prices, domestic economic conditions, and competitor prices) are significant in explaining domestic import prices.
Results from the extended exchange rate pass-through model, including the role of oil prices
Given that the ERPT coefficients are negative for the oil-importing countries, it can be inferred that the pass-through has the potential of lowering domestic import inflation. For oil-exporting economies, the evidence of positive ERPT means the pass-through tends to accelerate import inflation. It is in this light that we further extend the traditional approach to modelling ERPT to include the role of changes in oil prices (see Table 3). Similar to our earlier findings, the Hausman test results in Table 3 fail to reject the null hypothesis that the long-run elasticities are equal across the panel. Thus, the PMG yet again appears as a more efficient estimator for modelling ERPT. However, the estimated ERPT is rather insignificant in this case.
| TABLE 3: Exchange rate pass-through panel regression results (symmetric model with interaction term). |
Results from the traditional asymmetric exchange rate pass-through model
The insignificant role of oil prices in ERPT fluctuations to domestic prices observed in the previous section seems unusual, particularly in the context of the investigated economies. It contradicts the existing hypothesis that the relationship between exchange rates and prices depends on the shocks that cause the exchange rates to fluctuate as established in several previous studies (Forbes et al. 2016; Kirby & Meaning 2014; Mirdala 2014; Nakibullah & Bahrain 2016). Unlike these earlier findings, the asymmetry panel ERPT regression results in Table 4 show that asymmetries matter in the ERPT to domestic prices. In line with the standard practice in literature (see, e.g. Salisu & Ndako 2018), the Wald restriction test is employed to ascertain or refute the null hypothesis of no asymmetry. The study results reveal rejection of null hypothesis of no asymmetry in both long-run and short-run irrespective of whether the group is oil-importing or oil-exporting. This, therefore, is an indication that asymmetry matters in ERPT fluctuations to prices in the investigated economies.
| TABLE 4: Exchange rate pass-through panel regression results (asymmetric model without interaction term). |
The study finds the degree of pass-through quite alarming in the long run across the two economies, but its significance is rather evident in the net oil-exporting economies, where a positive shock to exchange rates records a complete pass-through to domestic import prices at 1.23% (more than 100%). Besides, more than 50% of negative shocks to exchange rates significantly pass-through to import prices of the selected net oil-exporting countries for the periods under consideration. The fact that the magnitude and/or degree of the pass-through is higher for positive than negative exchange rate changes is an indication that asymmetries matter for the degree of pass-through, particularly in the net oil-exporting countries. In the case of oil-importing countries, however, the pass-through is incomplete, but the significance of the pass-through is only evident when the shock to exchange rates is negative, particularly in the short run. Overall, accounting for asymmetries in ERPT is important when examining the extent to which fluctuations in exchange rates are being transmitted to domestic import prices in net oil-importing and oil-exporting nations.
Results from the asymmetric exchange rate pass-through model, including the role of oil prices
Having shown that asymmetries matter for the extent to which fluctuations in exchange rates pass-through to domestic import prices, particularly in the short run for oil-importing economies and in the long run for the oil-exporting group, we proceed to empirically investigate our hypothesis that the role of oil price changes as an accelerator of ERPT matters more when we capture asymmetries in the pass-through modelling framework. Similar to asymmetric ERPT without the role of changes in oil prices, the Hausman test results reaffirm the MG estimator as more efficient in the case of net oil-exporting economies, whilst the PMG is more efficient in the case of net oil-exporting economies. The Wald test results are also consistent in rejecting the null hypothesis of no asymmetry in both the long run and short run irrespective of whether the group is oil-importing or oil-exporting. This, therefore, is an indication that the extent to which asymmetries matter in the pass-through effect of exchange rate fluctuations is robust to the underlying source of functions, which in this case is measured as changes in oil prices. Contrary to our earlier findings, where the responsiveness of exchange rates to changes in oil prices exhibits no significant pass-through irrespective of which of the two economic groups is under consideration, the results in Table 5 suggest that the role of changes in oil prices as a potential accelerator of ERPT matters more when the pass-through is captured asymmetrically.
| TABLE 5: Exchange rate pass-through panel regression results (asymmetric model with interaction term). |
Conclusion and recommendation
This study has proposed an approach that should improve our understanding of and ability to capture the responsiveness of exchange rates to external price shocks and how these influence the degree of ERPT to domestic prices. Based on our empirical findings, we infer that taking exchange rate movements as exogenous in the pass-through specification (as often demonstrated in some empirical studies) tends to introduce a bias in the estimation of the modelling framework of the pass-through. In addition, we argue that understanding whether the pass-through is symmetric or asymmetric for a particular economy is essential in the evaluation of the responsiveness of exchange rate to shocks because of other external prices.
The study provides some insights on the likely inflationary implications of ERPT to domestic prices in both oil-exporting and oil-importing economies. For countries that rely on oil (either as major net oil-importers or oil-exporters), a pre-evidence-based policy option that takes cognisance of changes in oil prices as an accelerator of ERPT should form the core of monetary policy to mitigate any potential adverse effects of ERPT. Secondly, monetary policy designed to mitigate the potential adverse effect of ERPT fluctuations to inflation in the investigated oil-importing and oil-exporting countries should be rooted on the understanding of the direction of currency movements (positive or negative changes in exchange rate) which is more vulnerable to changes in oil prices.
Acknowledgements
The authors deeply appreciate the African Economic Research Consortium (AERC) for its financial support to carry out this research. They are also grateful to AERC reviewers and resource persons for their comments and suggestions that helped to shape the ideas presented in this study, consequently improving the overall quality of the article. However, the findings made and opinions expressed in this article are exclusively those of the authors. The authors are also solely responsible for content and any errors.
Competing interests
The authors have declared that no competing interests exist.
Authors’ contributions
O.J.A.’s contribution is 85%, and H.N.’s contribution is 15%.
Funding information
This study was funded by the African Economic Research Consortium (AERC), Ref: 17018.
Data availability statement
Data are available from the author upon reasonable request.
Disclaimer
The views and opinions expressed in the article are those of the authors and do not necessarily reflect the official policy or position of any affiliated agency of the authors.
References
Ahmad, A.H. & Hernandez, R.M., 2013, ‘Asymmetric adjustment between oil prices and exchange rates: Empirical evidence from major oil producers and consumers’, Journal of International Finance, Market, Institution and Money 27, 306–317. https://doi.org/10.1016/j.intfin.2013.10.002
Aloui, R., Aïssa, M.S.B. & Nguyen, D.K., 2013, ‘Conditional dependence structure between oil prices and exchange rates: A copula-GARCH approach’, Journal of International Money and Finance 32, 719–738. https://doi.org/10.1016/j.jimonfin.2012.06.006
Atems, B., Kapper, D. & Lam, E., 2015, ‘Do exchange rates respond asymmetrically to shocks in the crude oil market?’, Energy Economics 49, 227–238. https://doi.org/10.1016/j.eneco.2015.01.027
Athukorola, P. & Menon, J., 1995, ‘Exchange rates and strategic pricing: The case of Swedish machinery exports’, Oxford Bulletin of Economics and Statistics 57(4), 533–546. https://doi.org/10.1111/j.1468-0084.1995.tb00038.x
Bache, I.W., 2002, Empirical modeling of Norwegian of import prices, Norges Bank working paper No. 1.
Bailliu, J. & Eiji, F., 2004, Exchange rate pass-through and the inflation environment in industrialized countries: An empirical investigation, Bank of Canada Working paper, vol. 21.
Bal, D.P. & Rath, B.N., 2015, ‘Nonlinear causality between crude oil price and exchange rate: A comparative study of China and India’, Energy Economics 51, 149–156. https:doi.org/10.1016/j.eneco.2015.06.013
Barhoumi, K., 2006, ‘Differences in long-run exchange rate pass-through into import prices in developing countries: An empirical investigation’, Economic Modelling 23(6), 926–951. https://doi.org/10.1016/j.econmod.2006.04.006
Blackburne, E.F. & Frank, M.W., 2007, ‘Estimation of nonstationary heterogeneous panels’, Stata Journal 7(2), 197–205. https://doi.org/10.1177/1536867X0700700204
Bouoiyour, J., Selmi, R., Tiwari, A.K. & Shahbaz, M., 2015, ‘The nexus between oil price and Russia’s real exchange rate: Better paths via unconditional vs. conditional analysis’, Energy Economics 51, 54–66. https:doi.org/10.1016/j.eneco.2015.06.001
Breitung, J., 2000, ‘The local power of some unit root tests for panel data’, in B.H. Baltagi (ed.), Nonstationary panels, panel cointegration, and dynamic panels, pp. 161–177, Elsevier, Amsterdam.
Brun-Aguerre, R., Fuertes, A. & Phylaktis, K., 2012, ‘Exchange rate pass-through into import prices revisited: What drives it?’, Journal of International Money and Finance 31(4),818–844. https://doi.org/10.1016/j.jimonfin.2012.01.009
Burstein, A. & Gopinath, G., 2014, ‘International prices and exchange rates’, Handbook of international economics, 4th edn., pp. 391–451. Elsevier.
Bussie`re, M., 2013, ‘Exchange rate pass-through to trade prices: The role of nonlinearities asymmetries’, Oxford Bulletin of Economics and Statistics 75(5), 731–758. https://doi.org/10.1111/j.1468-0084.2012.00711.x
Campa, J. & Goldberg, L., 2002, Exchange rate pass-through into import prices: A macro or micro phenomenon? NBER working paper No. 8934.
Campa, J. & Goldberg, L. 2010, ‘The sensitivity of the CPI to exchange rates: Distribution margins, imported inputs, and trade exposure’, Review of Economics and Statistics 92(2), 392–407.
Campa, J.M. & Goldberg, L.S., 2005, ‘Exchange rate pass-through into import prices’, The Review of Economics and Statistics 87(4), 679–690. https://doi.org/10.1162/003465305775098189
Campa, J.M. & Gonzàlez, J.M., 2006, ‘The difference in the exchange rate pass-through in the Euros areas’, European Economic Review 50(1), 121–145. https://doi.org/10.1016/j.euroecorev.2004.12.002
Cheikh, N.B. & Rault, C., 2015, ‘Recent estimates of exchange rate pass-through to import prices in the euro area’, Review of World Economics 152, 69–105. https:doi.org/10.1007/s10290-015-0233-x
Chen, H., Liu, L., Wang, Y. & Zhu, Y., 2016, ‘Oil price shocks and US dollar exchange rates’, Energy 112, 1036–1048. https://doi.org/10.1016/j.energy.2016.07.012
Chou, K. & Tseng, Y., 2015, ‘Oil prices, exchange rate, and the price asymmetry in the Taiwanese retail gasoline market’, Economic Modelling 52(B), 733–741. https://doi.org/10.1016/j.econmod.2015.10.012
Choudhria, E.U. & Hakura, D.S., 2006, ‘Exchange rate pass-through to domestic prices: Does the inflationary environment matter?’, Journal of International Money and Finance 25, 614–639.
Choudhria, E.U. & Hakura, D.S., 2014, ‘The exchange rate pass-through to import and export prices: The role of nominal rigidities and currency choice’, Journal of International Money and Finance 51, 1–25. https://doi.org/10.1016/j.jimonfin.2014.09.006
Donayre, L. & Panovska, I., 2016, ‘State-dependent exchange rate pass-through behavior’, Journal of International Money and Finance 64, 170–195.
Forbes, K., Hjortsoe, I. & Nenova, T., 2016, The shocks matter: Improving our estimates of exchange rate pass-through, Bank of England External MPC unit discussion paper No. 43.
Fowowe, B., 2014, ‘Modelling the oil price-exchange rate nexus for South Africa’, International Economics 140, 36–48. https://doi.org/10.1016/j.inteco.2014.06.002
Ghosh, A., 2013, ‘Exchange rate pass-through, macro fundamentals and regime choice in Latin America’, Journal of Macroeconomics 35, 163–171. https://doi.org/10.1016/j.jmacro.2012.09.001
Hadri, K., 2000, ‘Testing for stationarity in the heterogeneous panel’, Econometrics Journal 3(2), 148–161. https://doi.org/10.1111/1368-423X.00043
Harris, R.D. & Tzavalis, E., 1999, ‘Inference for unit roots in dynamic panels where the time dimension is fixed’, Journal of Econometrics 91(2), 201–226. https://doi.org/10.1016/S0304-4076(98)00076-1
Im, K.S., Pesaran, H. & Shin, Y., 1997, Testing for unit roots in the heterogeneous panels, Working paper 9526, University of Cambridge, DAE.
Jiang, J. & Gu, R., 2016, ‘Asymmetrical long-run dependence between oil price and US dollar exchange rate-based on structural oil shocks’, Physica A 456, 75–89.
Jiang, J. & Kim, D., 2013, ‘Exchange rate pass-through to inflation in China’, Economic Modelling 33, 900–912. https://doi.org/10.1016/j.physa.2016.03.016
Jimborean, R., 2013, ‘The exchange rate pass-through in the new EU member states’, Economic Systems 37(2), 302–329. https://doi.org/10.1016/j.ecosys.2012.08.006
Karagoz, M., Demirel, B. & Bozdag, E.G., 2016, ‘The pass-through effect from exchange rates to the prices in the framework of inflation targeting policy: A comparison of Asia-pacific, South American and Turkish Economies’, Procedia Economics and Finance 38, 438–445.
Kirby, J. & Meaning, S., 2014, ‘Exchange rate pass-through: A view from a global structural model’, National Institute Economic Review 230, 59–64.
Le, T. & Chang, Y., 2011, Dynamic relationships between the price of oil, gold, and financial variables in Japan: A bounds testing approach, MPRA paper No. 33030.
Levin, A., Lin, C.F. & Chu, C., 2002, ‘Unit root tests in panel data: Asymptotic and finite-sample properties’, Journal of Econometrics 108(1), 1–24. https://doi.org/10.1016/S0304-4076(01)00098-7
Maddala, G.S. & Wu, S., 1999, ‘A comparative study of unit root tests with panel data and a new simple test’, Oxford Bulletin of Economics and Statistics 61(S1), 631–652. https://doi.org/10.1111/1468-0084.61.s1.13
Marazzi, M. & Sheets, N., 2007, ‘Declining exchange rate pass-through to US import prices: The potential role of global factors’, Journal of International Money and Finance 26(6), 924–947. https://doi.org/10.1016/j.jimonfin.2006.12.003
Mirdala, R., 2014, ‘Exchange rate pass-through to consumer prices in the European transition economies’, Procedia Economics and Finance 12, 428–436. https://doi.org/10.1016/S2212-5671(14)00364-5
Mohammed, K., Bendob, A., Djediden, L. & Mebso, H., 2015, ‘Exchange rate pass-through in Algeria’, Mediterranean Journal of Social Sciences 6(2), 195–201. https://doi.org/10.5901/mjss.2015.v6n2p195
Olivei, G.P., 2002, ‘Exchange rates and the prices of manufacturing products imported into the United States’, New England Economic Review (Q1), 3–18.
Park, J. & Ratti, R.A., 2008, ‘Oil price shocks and stock markets in the US and 13 European countries’, Energy Economics 30(5), 2587–2609. https://doi.org/10.1016/j.eneco.2008.04.003
Pesaran, H., 2007, ‘A simple panel unit root test in the presence of cross-section dependence’, Journal of Applied Econometrics 22(2), 265–312.
Pesaran, M.H., Shin, Y. & Smith, R.P., 1997, Estimating long-run relationships in dynamic heterogeneous panels, DAE working papers amalgamated series 9721.
Pesaran, M.H., Shin, Y. & Smith, R., 1999, ‘Pooled mean group estimation of dynamic heterogeneous panels’, Journal of the Phillips and Perron 94(446), 621–634. https://doi.org/10.1080/01621459.1999.10474156
Pesaran, M.H. & Smith, R.P., 1995, ‘Estimation of long-run relationships from dynamic heterogeneous panels’, Journal of Econometrics 68(1), 79–113. https://doi.org/10.1016/0304-4076(94)01644-F
Reboredo, J.C., 2012, ‘Modelling oil price and exchange rate co-movements’, Journal of Policy Modeling 34(3), 419–440. https://doi.org/10.1016/j.jpolmod.2011.10.005
Salisu, A.A. & Isah, K.O., 2017, ‘Predicting US inflation: Evidence from a new approach’, Economic Modelling 71, 134–158. https://doi.org/10.1016/j.econmod.2017.12.008
Salisu, A.A. & Ndako, U.B., 2018, ‘Modeling stock price–exchange rate nexus in OECD countries: A new perspective’, Economic Modelling (in press). https://doi.org/10.1016/j.econmod.2018.05.010
Shin, Y., Yu, B. & Greenwood-Nimmo, M., 2014, ‘Modelling asymmetric cointegration and dynamic multipliers in a nonlinear ARDL framework’, in W. Horrace & R. Sickles (eds.), The festschrift in honor of Peter Schmidt: Econometric methods and applications, pp. 281–314. Springer, New York. https://doi.org/10.1007/978-1-4899-8008-3_9
Turhan, M.I., Sensoy, A. & Hacihasanoglu, E., 2014, ‘A comparative analysis of the dynamic relationship between oil prices and exchange rates’, Journal of International Financial Markets, Institutions Money 32, 397–414.
Uddin, K.M.K., Quaosar, A.L. & Nandi, D.C., 2014, ‘The impact of depreciation on the domestic price level of Bangladesh’, Journal of Economics and Sustainable Development 5(25), 108–114.
Yang, L., Cai, X.J. & Hamori, S., 2017, ‘Does the crude oil price influence the exchange rates of oil-importing and oil-exporting countries differently? A wavelet coherence analysis’, International Review of Economics and Finance 49, 536–547. https://doi.org/10.1016/j.iref.2017.03.015
|

