Abstract
This article investigates the industrial success of various cities in KwaZulu-Natal, South Africa. It assesses the hypothesis that knowledge spillovers are supportive of industrial growth at the city level. Theories of economic city growth suggest that cities are engines of knowledge spillovers, which are essential to generate growth. This study utilised data on the growth of industries in cities in KwaZulu-Natal between 1996 and 2015. The study initially found that industries develop better in environments characterised by less concentration and more city diversity, which gave evidence of Jacobs’ externalities. However, after controlling for industry-specific and city-specific characteristics, the results changed significantly. No evidence was found for concentration effects (Marshall/Arrow/Romer-externalities) and less diversity supports city-industry growth (evidence against Jacobs’ externalities).
Introduction
Why do some industries succeed in some cities while others do not? Provinces such as KwaZulu-Natal (KZN), South Africa; rural and urban settlements; and towns and cities are important to facilitate development in their immediate surrounding areas. As such, the province is an integral part of the national spatial economic system. Cities and towns therefore matter because this is where economic activity occurs. With its local city-industries, it is where production and consumption occur and the allocation of resources predominantly takes place. Innovations and technological progress are also more likely to originate in these towns and cities. Towns and cities are therefore very relevant in the modern economy and therefore the factors that determine the economic growth of a town or city are important.
Cities offer people opportunities to learn and gain experience and this improves individual productivity (Glaeser et al. 1992). This leads to higher income and living standards, justifying the higher rent that cities demand. An easier flow of ideas activates innovation and progress and guarantees the continuation of cities, regardless of higher rent. The work by Glaeser et al. (1992) fits well with recent research regarding the underlying theories of city economies.
The majority of city-economic growth theories view knowledge spillovers and other externalities as the main determinants of progress (Kleynhans 2016). It is based on the argument that an easier flow of ideas enables easy flow of knowledge spillovers, which leads to economic growth in cities (Kleynhans & Swart 2012). Intellectual knowledge flows much easier between industries located in close proximity than across oceans.
During the last 30 years, there has been much variation between the growth rates that cities in the United States experienced (Glaeser, Scheinkman & Shleifer 1995). The population size of some cities grew a great deal, while others virtually disappeared. This suggests that this variation in growth experiences may be because of geography and migration to the south and west; however, they found the economic forces in cross-sections of the country difficult to explain.
The majority of analyses on city growth consider economic forces and are based on regional development studies that include research by Mills (1995), Kain and Neidercorn (1963) and Borts (1960). Numerous studies, such as Kleynhans (2006), Jacobs (1969), Chinitz (1962) and Marshall (1890), focus on human capital as the most important determinant. The argument that views human capital as a major factor stimulating economic growth is also supported by Lucas (1988) and Romer (1986), who regard knowledge spillover as an ‘engine of growth’. According to Bernstein and McCarthy (2005) and Kleynhans and Drewes (2008b), competent local governance and entrepreneurship are drawn to locations where the lifestyle, existing technology and natural resources are conducive to growth.
This study assesses the supposition that knowledge spillover enhances city-industry growth. The study seeks to determine which sectoral economic structures lead to a growth in employment of various city-industries. The study will focus on cities, both rural and urban, in the KZN province of South Africa.
This article is structured as follows: The following section provides a description of the three major theories related to the city economy, and the ‘The role of dynamic externalities’ section considers theories of dynamic externalities. Then, the variables and data used in this study are described, followed by the ‘Facts about diversity and concentration in KZN cities’ section, which tested the most important conventional assumptions concerning the way cities are organised, their magnitude and geographic positioning. The ‘Constructing and evaluating the panel’ section focuses on the construction and evaluation of the panel, while the ‘Empirical analysis’ section presents the results of the empirical analysis. The article ends with a conclusion.
Economic theories relevant to city-industry growth
The majority of economic theories consider localisation and urbanisation economies as the most important benefits of cities. Localisation economies regard the advantages that firms enjoy being in proximity of other industries, especially similar industries. Industries promote knowledge exchange between associates of various firms. Localisation economies cause dynamic Marshall/Arrow/Romer (MAR) externalities because places where city-industries are over-represented stimulate faster industrial growth (see Arrow 1962; Blein & Suedekum 2005; Marshall 1890; Romer 1986).
The advantages that the diversity and scale of cities offer are studied in urbanisation economies. Urbanisation economies relate to the so-called dynamic Jacobs’ externalities, which occur where industries develop faster than others when they had been surrounded by comparatively diversified industrial structures over a long time. According to these theories, cross-fertilisation of labour from different professional backgrounds offers superior knowledge spillovers (Blein & Suedekum 2005).
The primary theories relative to the city are briefly discussed in the ‘Urban economic theory’ section, with specific reference to the possible factors that support or reduce city and city-industry growth.
Urban economic theory
Urban economics explain spatial science and how urban systems function. Among the pioneers in this field were researchers such as Muth (1969), Alonso (1960), Isard (1956) and Von Thünen (1842), among others. The interactive structure of special economies and its growth causes various externalities, which are also essential for sustained future city growth. Researchers distinguish between externalities that are associated with specialisation, called MAR externalities; externalities caused by the socio-economic diversity where synergy leads to economic advantages known as Jacobs’ externalities; and Porter externalities that are related to the competitive forces that lead economic agents in close proximity to be innovative and more competitive (Nijkamp 2009).
Urban economics explain that economic agents, such as city-industries, are close together and in competition with each other. This forces them to find a specific niche where each can specialise in a specific activity and create products or services in a modern way that would attract buyers of their products (Kleynhans & Drewes 2008a). As so many social and cultural groups are concentrated together, agents can learn from each other and also enjoy common synergies (Nijkamp 2008). This constitutes the three externalities mentioned above.
Based on the main externalities, the density of cities leads to the principles of accessibility, spatial interaction, urban hierarchy, agglomeration and competitiveness (Nijkamp 2009). Close proximity of economic agents leads to easy access and interaction, causing the costs of mobility and land use to be lower than elsewhere. As economic agents are located close to one another, contact between them is easy, fast and more frequent, leading to economic and spatial consequences. The heterogenic nature of cities then causes a new hierarchy to develop where new disparities of residential development and divisions of labour emerge, with socio-economic implications. The close proximity of people and density of production lead to agglomeration advantages, which lead to higher productivity, efficiency, profits and welfare. Rent gradients may, for example, create concentric patterns and specialised territorial configurations. Agglomeration yields knowledge and technological spillovers, which make industries locally and internationally more competitive (Kleynhans 2016).
Density of city economies yields advantages related to costs and efficiency, as well as regional and national advantages, also known as principle benefits (Camagni 1992). The main spatial principles are those related to competitiveness, agglomeration, a special new hierarchy, accessibility and interaction. Urban efficiency mechanisms develop and build competitive advantage because of the agglomeration of people and firms in cities where ideas develop continuously, leading to a constant flow of new innovations, where specific services and goods answer specific needs. Because there is a high concentration of economic activity and in propinquity, it offers special advantages of agglomeration, such as spillover effects, easy access to supplies, better rent gradients and transaction costs. Accessibility leads to easy access of inputs and supplies, and markets offer cheaper mobility and lower land-use costs in cities. All these factors create a unique urban hierarchy where labour is applied differently and the residential setup differs widely from the rural. This not only creates new opportunities to prosper but also increases the socio-economic inequality in many cases.
Theory of new economic geography
The realisation that regional factors have an influence on the economy and how economies develop through space and time is a concept already known to economists but greatly neglected (Eckey & Kosfel 2004). Marshall (1890) studied it long ago and Krugman (1991) reinvented it recently, naming it the new economic geography (NEG) (Kleynhans & Drewes 2008b). It considers the effect of clustering and aggregation of economic activity through geographical space, and also which factors could disrupt its equilibrium.
It originally developed a simplified competitive model of an economy consisting of two manufacturing sectors. On the one hand, it considers the classic characteristic of markets to find equilibrium through space, but there are also propensities of instability and polarisation through agglomeration. Free market economies always move back to a place of equilibrium following a disruption, but it is also possible that feedback effects could cause a circular chain of events that could reinforce the influence of that disturbance, which shifts the economy even further from the original position of equilibrium (Eckey & Kosfel 2004).
In the NEG, the theory usually starts by considering two regions at an equal level of development (Krugman 1991). Some economic shocks or changes then occur in one of these economies. Classical economics dictate that there will be market movements to restore the disturbance. Polarisation theory suggests, however, that linkage may cause the level of economic activity of the two regions to deviate even further from each other through space. A firm might become bankrupt and be forced to leave the industry. This could, however, force another entrepreneur to fill the demand gap that occurred, elsewhere. Labourers will then be attracted to that new firm and will also relocate to their new residences. Wealth, wages and income will therefore shift through geographical space from one region to another, causing disequilibrium between the development statuses of these two regions. This will also be amplified through the multiplier effect causing the gap between production, income and market demand of these regions to continue to grow larger. The process will also spread to other sectors such as residential, retail and other services. Consequently, the level of development will be transferred from one region to the other region. One will enjoy the added agglomeration of wealth, while the other would suffer. As high economic development in a certain region becomes more attractive, it will reinforce and sustain the growth in the said region, at the cost of the other. Negative externalities, such as rising prices of property, environmental degradation and the overloading of infrastructure, may cause some counter balance but never enough to curb the inequality in regional development patterns that developed (Eckey & Kosfel 2004).
Firms may also be established near households when residential areas are already concentrated (Courtney, Lépicier & Schmitt 2005). This may decrease transport costs and provide larger market access. Households tend to locate near firms for the same reasons. It provides a wider range of products and lowers the cost of getting to work, shops and schools (Krugman 1991). The spatial concentration and advantages of production are known as the ‘home market effect’. Firms gain because of the larger market as they can sell their goods, shorten delivery distances and lower travelling costs of employees (Kleynhans & Drewes 2008b). At the same time, local input markets relate positively to the number of firms in a region using such inputs, implying that local purchasing propensity correlates with larger input markets (Krugman & Venables 1995).
The economic activity over a large geographical area therefore experiences internal spatial differences between regions, where market equilibrium may differ. This may yield increasing returns to some market agents and regions and imperfect competition in others. The difference in employment, consumer markets, producers and employment opportunities has a significant effect as spatial distance becomes important owing to the difference in economic activity between regions. This mobility of consumers, firms, employees and other factors of production may lead to the agglomeration of some regions and the deterioration of others (Fujita & Mori 2005).
New urban economics
Until the late 1960s, research on the economies of cities was mainly descriptive, but as the ‘New Urban Economics (NUE)’ developed, economists started to employ more rigorous methods of analysis. A mathematical approach gave a deeper understanding of how economic systems of cities operate and it developed a methodical framework for the future analysis of urban systems. Ideas could now be verified quantitatively (Button 1998).
Modelling the dynamics of urban growth mathematically has strong analytical power and researchers, such as Muth (1961), Beckmann (1969) and Mills (1995), stated to design elegant small models that could provide more insight. It usually assumed a single point, such as a transport node or shopping area, surrounded by residential housing. These models explain much in abstract terms, but they have inherent limitations because of their restrictive assumptions, which restrict their application to real-life situations. Especially when metropolitan areas began to restructure during the 1990s, their utility began to be outdated. Instead of only offering housing, simple retail and quality of life, the periphery of cities and suburban areas now also began to offer employment away from the traditional city centres (Button 1998).
The role of dynamic externalities
Regional development usually entails dynamic externalities, which are explained in various ways. When firms are in close proximity, their profits and economic progress are higher (Kleynhans 2016; Porter 1998). Many firms and people together generate more ideas that develop into new innovations, which are employed in production and increase productivity, which in turn yields higher profits, income and wealth. Where those new innovations are already employed, the knowledge and technology spill over to other firms in the region and all enjoy the economic benefits owing to their agglomeration.
They experience dynamic externalities, which were already introduced above; the first being MAR externalities, which focus on knowledge spillovers and specialisation (Glaeser et al. 1992). The MAR theory also indicates that in the local regional economy, the advantages of monopolies exceed competition. Porter (1998) supports the MAR theory and argues that these spillovers enhance industrial development. Porter differs, however, with the second assumption and stresses that competitiveness on the local scene is essential to enable the absorption of new innovations and apply it beneficially to local regional production. He affirms that regional monopolies are detrimental in this regard. Jacobs (1969) differs from the previous researchers and regards diversity and heterogeneity in a particular geographical space as the most important drivers of knowledge, growth and development. Away from the core industries with their specialised ways of doing things, ideas and new innovations are not limited to the set ideas and protocols already existing. Thinkers are therefore free to invent and apply new ventures and apply new methods, thereby creating new technologies providing them with a competitive edge.
The approaches to externalities considered above can be conceptualised in a model that can guide the analytical research. The local growth rate in local employment is the sum of growth in local wages, and technological progress, both locally and nationally. The local technological progress, in turn, is the result of the technological externalities present in a particular industry of a specific city. The model allows the user to determine the level of diversity, specialisation and local monopolies in an urban setting. The model can be summarised as:
where L represents the labour input, at specific time t, with w wages, and A represents changes in technology in nominal terms, while g is the dependency rate of the technological externalities present in an industry of a particular city. The assumption is that technological growth depends on exogenous factors, which include price movements, national technological changes at the firm and industry level, as well as externalities and knowledge spillovers. Knowledge spillovers also depend on local concentration, monopolies and diversity (Kleynhans 2016), which are easily estimated with this model. The model does, however, assume that knowledge spillovers remain constant over time for all firms, new and old, which may be too restrictive (Glaeser et al. 1992).
The model gives the impression that regional concentration suppresses city-industry growth, while diversity promotes it. City-industries where higher competition is prevalent will also facilitate higher growth than those that are less competitive. These general findings are also in line with other research results, including the current study.
Glaeser et al. (1995) examined the association between city growth, the growth in population, income and other specific economic features between 1960 and 1990.
They examined 203 large US cities and considered their change in relation to the size of their population, income, inequality, the labour force’s level of education, racial makeup, unemployment, production content, government size and several other factors. Their primary purpose was to understand which cities grew. Cities were treated as individual economies, using the nation’s communal force of labour and capital resources. City growth was therefore studied as a function of their citizenry’s level of satisfaction and the productivity of their labour force. Exogenous factors, such as talents of the labour force and propensity to save, were therefore ignored.
Labour income, life quality and therefore total utility of a particular city were then modelled as the:
Labour income of a potential migrant as the marginal product of labour:
where Ait is the level of productivity in city i and time t, Lit refers to the population of city i at time t, while σ represents the production parameter that needs to be estimated.
Quality of life is determined by an index (Q), where ς > 0 and Q summaries a wide range of factors:

And the Total utility of the potential migrant to the city i:
Glaeser et al. (1995) utilised population growth as the primary variable to estimate city growth. Income growth is also assumed to be an appropriate measure of city growth; however, it is less appropriate to determine progress as it also captures factors such as the deterioration of quantity of life. The population growth rate in logarithmic form is estimated as the primary dependent variable, using regression models, yielding various economic determinants of city growth.
Their research found that urban trends in growth in income and population are closely correlated. The initial level of education promotes city growth, while unemployment influences it negatively. Except for sanitation and government debt, which promote growth, expenditure by government did not reveal any relationship. Migration and city growth are also affected by several other attributions, such as the kind of weather.
Determinants of economic growth of municipalities in the United States were also researched by McGregor and Liner (2002) for the same period. Neoclassical economics predict per capita income convergence, and testing this hypothesis formed another major objective of their research. They found that municipalities are more specialised in some regards compared to the national level and that they are open economies between which labour and other recourses can move freely, supporting the neoclassical assumptions. This directly implies fundamental differences between the national and local economy and each therefore requires its own focus as suggested by this study. The inclusion of regional dummy variables in their research contained problems owing to the differences in spatial economic development in the United States over the research period.
McGregor and Liner (2002) found a positive relationship between the growth of a city and its initial levels of schooling, as well as its initial rate of employment. With low employment levels, population growth rises and vice versa. They could, however, not confirm a negative link between the growth in population and initial municipal employment but did confirm the notion that higher levels of education promote economic growth in cities. Using sensitivity analysis, they established that a 10% rise in the level of education leads to a 5% growth in income and a 7% growth in population figures.
The following section explains the variables and data that were used to determine the city-industry growth of KZN.
The variables used in this study
The theories on city economics and dynamic externalities suggest that city-industry diversity, an industry’s level of specialisation in a particular city and its degree of competition have a major influence on the rate of employment and economic growth of that city.
The local relative-specialisation index constitutes a measuring instrument for specialisation or concentration of a city-industry. It represents the share of employment a city-industry uses in a particular city, proportional to the employment share that the industry uses of the entire labour force in the region or province (Duranton & Puga 1999; Glaeser et al. 1992). Specialisation or concentration can therefore be expressed as:
This specialisation variable (LRS) indicates the level of industrial specialisation of a particular city. It shows the level of specialisation in relation to the rest of the province, if the assumption is made that employment of that industry was randomly scattered in that province. If an industry has a high specialisation index in a particular city, MAR externalities and Porter assume that that industry will enjoy high growth in that specific city (see Glaeser et al. 1992).
The level of competition an industry experiences locally in a particular city is determined by the number of companies per employee of an industry in that city, proportional to the number of companies per employee in that industry province-wide. The number of companies in city-industries and provincial-industries is unfortunately not available for KZN. Because the current research had so few variables available, the best alternative to the number of firms, with regard to the measuring of competition, is using the gross operating surplus (GOS). Gross operating surplus is defined by EuroStat (2017) as:
Gross operating surplus is the surplus generated by operating activities after the labour factor input has been recompensed. It can be calculated from the value added at factor cost less the personnel costs. It is the balance available to the unit which allows it to recompense the providers of own funds and debt, to pay taxes and eventually to finance all or a part of its investment.
And by Global Insight (2017) as the:
Gross Operating Surplus refers to the portion of GDP-R that is attributed capital. GOS is calculated as the difference between GVA-R and Labour Remuneration for each sector in each region.
To an extent, GOS is economic or abnormal profit and therefore indicative of the level of competition within the particular industry. For the purpose of this article, it will be assumed that the larger the GOS, the larger the surplus per employee and the less competitive that particular industry and vice versa. With less competition, prices are higher and income increases. Competition can therefore be estimated as:
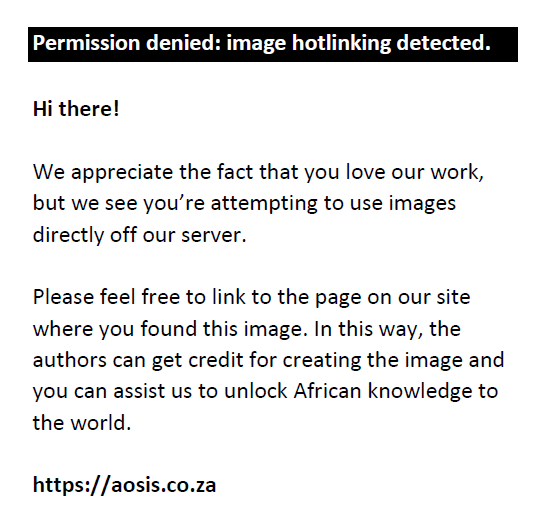
The degree of competition in the city-industry is therefore determined as the share of GOS per worker a specific city-industry uses in a particular city, proportional to the GOS per employee share of the industry in the province. An index below unity implies that this city-industry is more competitive in that particular city than elsewhere in the province. A liberal interpretation of this figure is then that a lower competition index is an indication of a larger growth rate. A value smaller than 1 implies that the city-industry produces less GOS per worker in relation to its size in that particular city than province-wide. A value larger than unity implies more monopoly businesses, which is detrimental to growth. The lower this value, the more competition is present in the market, promoting economic growth.
A diverse variety of industries in a particular city, as well as elsewhere, is essential for growth, according to Jacobs’s theory. The indicator for diversity is estimated as the ratio between the employment figures of the largest six industries in a specific city, in relation to the rest of the employment of the city not included in the specific industry under study. Diversity is therefore estimated as:
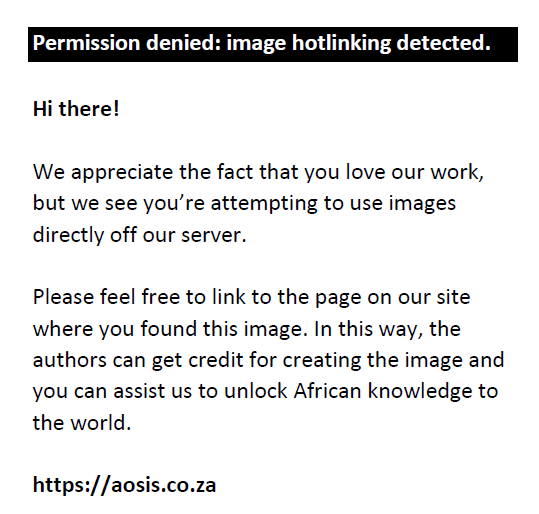
Industries with very low diversity indices grow the fastest. A lower diversity indicator implies a more diversified city, which is, according to Jacob’s theory, essential for industrial growth in a city (Glaeser et al. 1992; Jacobs 1969).
The data utilised
The data set utilised in the current study was compiled from the Global Insight Southern Africa’s (2017) Regional Explorer database and from the census data produced by Statistics South Africa (1996; 2016). Where possible, this data were augmented and supported by a database created and maintained by the author at the KZN treasury. The 1996 data set is the first with comprehensive figures and the 2015 figures are the newest figures available. It must be stated that 19 years might not be sufficient, that the reliability of the data in some cases is questionable and that this could pose some restrictions on the reliability of the research results.
The data used include employment figures, labour remuneration and GOS for each municipality in KZN (on a one-digit ISIC industry code). Wages were obtained by dividing labour remuneration by employment. The data are on a municipal level and not on a city level, simply because no such data on a city level is available. However, almost all municipalities in the province follow the typical polycentric city model as conceptualised by the NEG and NUEs theories, and it is therefore possible to argue that the municipalities are basically an extension of the basic polycentric cities. It is therefore possible to relate the municipal data to the city level. All data are in nominal terms.
It must also be stated that the quality of economic data is a cause of concern because of the limited amount of quality economic data at the sub-national level. This limitation is also emphasised by Luus and Krugell (2005) in their similar study. The current article will predominantly follow the methodologies employed by Glaeser et al., (1992), Glaeser et al. (1995) and Lu et al. (2013).
There are 51 municipal regions and 1 metropolitan region in the province, implying 52 cities in the province. The cities range from very small to very large in terms of population size; however, all cities generate economic activity and are therefore characterised by some sort of business structure. All of these cities achieved either positive or negative employment growth rates, with some sectors in some cities experiencing significantly more growth than others, while in some cities certain sectors experienced negative growth rates, while the same sector experienced positive growth rates in other cities.
Tables 1–4 present a description of the panels used. Panel A (Table 1) shows the six smallest and the six largest cities in terms of total employment in 1996 and the six largest industries in each city. The largest city, eThekwini (or Durban), had employment exceeding 758 000 and the smallest town, Hluhluwe, had a working population of approximately 1500. A large variety of major industries is represented in the data set, with most also containing features of services-related industries.
| TABLE 1: Description of the data: Panel A – 1996 cities. |
| TABLE 2: Description of the data: Panel B (included city-industries in the 12 cities). |
| TABLE 3: Description of the data: Panel C (most common city-industries in the 12 cities). |
| TABLE 4: Description of the data: Panel D (city-industry growth in the 12 cities). |
The top city-industries in the panel for 1996 are shown in Panel B (Table 2), both in absolute and relative terms. It indicates that total employment in the textile, clothing and leather goods industries in these 12 cities has decreased significantly over the period, whereas total employment in the education and other business activities industries has increased significantly. Of the total employment in the province during 1996, a total of 40% were employed in the province’s 12 city-industries, which decreased to 36% in 2015.
The most common industries in the 12 cities and the number of appearances of each during 1996 are provided in Table 3. Education is the most common city-industry, appearing in all 12 cities. A few other primary and secondary industries also appear, but the most common industry related to population is the tertiary sector (63% [1996] and 74% ([2015]).
The six fastest-growing and six declining city-industries among the 12 cities in terms of employment are provided in Table 4. The panel illustrates that city-industries have a larger growth rate where concentration is less and diversification of city-industries and the industrial competition are higher. This can be interpreted as counterevidence against MAR externalities and as evidence in support of Jacobs’ externalities. These impressions form the basis of the empirical analysis.
Facts about diversity and concentration in KwaZulu-Natal cities
The existing literature represents a set of stylised facts concerning the size, location and composition of cities (Duranton & Puga 1999). The current study will focus on four such facts.
The first fact implies that cities that strongly specialise in a few activities usually exist together with cities that are much more diversified. This also seems to be true for KZN; for example, the diversity and concentration rankings of the 12 cities as displayed in Table 5 (where ‘1’ is least diversified and most concentrated). The findings suggest that specialisation and diversity patterns are strictly random. Pearson’s product moment correlation coefficient is very low, suggesting that the correlation between diversity and concentration is not statistically significant at a 1% level.
| TABLE 5: Most and least specialised and diversified KwaZulu-Natal cities. |
The second fact relates to city size and diversity assuming that larger cities are more diversified (Duranton & Puga 1999). This also seems to be true for KZN; for example, the diversity and concentration rankings of the 12 cities are displayed in Table 6. The table suggests that the largest KZN cities are the most diversified. The product moment correlation coefficient of Pearson is very high and statistically significant at a 1% level.
| TABLE 6: Size diversity of KwaZulu-Natal cities. |
The assumption that relative and individual data on the sizes of cities, specialisation and their rankings have a stable distribution over time (Duranton & Puga 1999) seems to be true for KZN in that the distribution of city size seems very stable. Table 7 indicates that that the Pearson product moment correlation coefficient is very high and statistically significant at a 1% level.
| TABLE 7: The relative city size of KwaZulu-Natal cities. |
The relative size of cities is quite stable, and there is a strong persistence of the same activities in particular cities (Duranton & Puga 1999). Table 8 suggests that significant changes with regard to the diversity patterns within the cities occurred between the two periods, but that the patterns of specialisation tend to continue over time.
| TABLE 8: Diversity relation and city specialisation relation of KwaZulu-Natal cities. |
The last fact states that the growth of specific cities correlates to their relative location and individual specialisation and diversity. Glaeser et al. (1992) aimed to determine whether continuous growth is stimulated by diversity. They determined that in US cities local competition and diversity promote job creation, while specialisation destroys jobs. The results presented in Table 9 indicate that the city population growth in KZN is not statistically significantly correlated with diversity, specialisation or competition. City diversity in KZN is, however, statistically significantly positively correlated to city-economic growth, which implies that a decrease in diversity supports city-economic growth. The KZN results seem to be in contradiction with the international results.
| TABLE 9: City growth specialisation, diversity and competition in KwaZulu-Natal cities, 1996 to 2015. |
Constructing and evaluating the panel
The research sample includes 72 observations of the six fastest and slowest-growing industries between 1996 and 2015, in the six largest and smallest cities in the KZN province in terms of employment. The descriptive statistics of the panel data are displayed in Table 10. It indicates that the concentration, diversity and competition variables are not normally distributed (p < 0.05), while employment growth rate (Emplrlog), initial employment (Empl96) and initial average wage rate (Wagel96) in log format are normally distributed (p > 0.05). The mean of the log employment growth rate is 0.23, suggesting marginal average growth in the sample employment. Dispersion of growth over the various city-industries is significant, as indicated by the standard deviation of 0.35. This may also be an indication that some primary and secondary industries, as well as services in the provincial economy are declining.
Table 11 provides the correlations between the key variables, which suggest that concentration and diversity have a negative (inverse) statistically significant relationship with city-industry employment growth. This is also consistent with the findings of Table 4 (Panel D), while competition has a positive statistically significant relationship.
Empirical analysis
The current research closely followed the methodology employed by both Glaeser et al. (1992) and Lu et al. (2013) estimating the link between concentration and diversity theories of the city-industry growth and the province of KZN from 1996 to 2015. The equation to be estimated will include the same control variables with the base year being 1996. Lu et al. (2013) estimated the applicability of concentration and diversity theories to city-industry growth rates in China, using the equation:
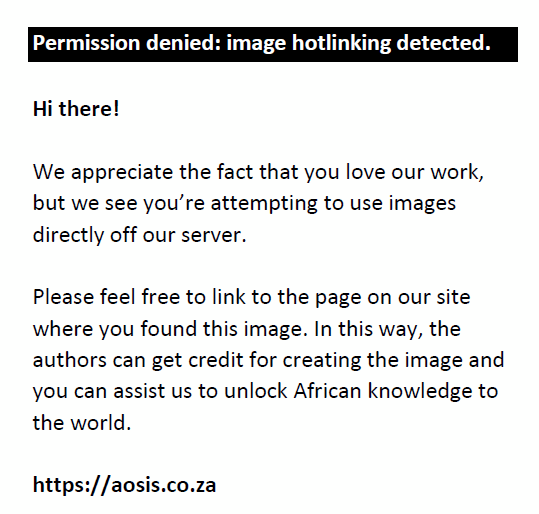
where X′ic is a vector of control variables. They included control variables consisting of: the initial city-industry employment (log) in industry i and city c in a particular year, which accounts for the possible catching-up effects; average wage (log) in industry i and city c in that year to compensate for the possible migration of workers to areas of higher wages, or firms moving to areas accepting lower wages; and the degree of competition of industry i in city c of that year, which is measured by the number of firms per worker of industry i in city c relative to the number of firms per worker of industry i present nationwide.
The benchmark estimation results of the current study, in which concentration and diversity of the city-industry economies of KZN are determined using the employment data, are provided in Table 12. It employed the equation above using employment growth as the dependent variable. In the alternative, GDP growth was used as the dependent variable. Columns 1 and 2 show concentration and diversity separately, while column 3 shows it together.
| TABLE 12: Main results of KwaZulu-Natal city-industry economies. |
The research results show a statistically significant negative coefficient of concentration, as well as diversity in KZN, but only when considered separately. Accordingly, the industrial growth rate is higher in cities with larger diversity and less concentration. These findings corroborate the diversity theory but contradict the concentration theory.
There are various industry and city characteristics, which were not available in the analysis, which might cause some bias. There may be some features that correlate with the indicators of city-industry diversity and concentration, leading to a situation where E(Concentration. εic) ≠ 0 and E(Diversity. εic) ≠ 0 (Lu et al. 2013). To compensate for this concern, dummies are added for industries and cities, and the equations estimated again (similar to Lu et al. 2013). This has a substantial influence on the research results, as shown in column 4 of Table 12. Specifically, concentration is not significantly correlated to industrial city growth anymore, and lower diversity becomes positively correlated to industrial city growth with statistical significance. This affirms that industrial growth in cities increases as city-industry diversity decreases, but concentration is now irrelevant. The difference in the research findings when specific industry and city attributes in the form of dummies are added to the regression analysis highlights the importance to account for all specific aspects of cities and industries when considering growth.
The existing literature uses output data as proxy for city-industry concentration and diversity in Lu et al. (2013). Our study therefore also used output data (GDP growth rate in logs) to answer the research question. The analysis was then re-estimated and the results of equations 3 and 4 provided in Table 12. With regard to the re-estimated equation 3, concentration continues to be statistically significant (inverse relationship with coefficient = −0.02), while diversity has an inverse relationship (coefficient = −0.02), but not statistically significant. The results suggest that the main results remain robust, but when considering equation 4, both concentration and diversity are statistically insignificant when using output data, raising some concerns about the robustness of the main results.
The measure of competition in the benchmark estimation of the current study is the GOS per labourer of a particular industry in a specific city relative to the industrial totals of the province. To ascertain the robustness of the study, national totals were used in the estimation of the degree of competition. The main findings remained relatively constant when employment and output data were employed. The findings did not differ much from our previous results – that concentration has an inverse and statistically significant impact on growth, while diversity is not significant.
Including the dummy variables has the exact opposite effect in that the impact of less diversity is positive and statistically significant, while the impact of concentration is not significant.
Conclusion
This article investigated and compared the role that industrial growth plays in the growth of cities in KwaZulu-Natal Province (KZN), South Africa. Employment growth in city-industries can be regarded as a function of dynamic externalities. The MAR externalities contend that a highly concentrated industrial environment is conducive to high city-industry growth, while localisation economies are consistent with intra-industrial knowledge spillovers, and Jacobs’ externalities suggest diversification as the key to city-industry growth. Urbanisation economies also assume that inter-industrial knowledge spillovers facilitate more knowledge exchange between specialists from different industries. This article therefore estimated the levels of concentration and diversity of the various city-industries in the six largest and six smallest cities in the province of KZN in terms of employment growth.
The initial analysis and econometric research results suggest that at the city-industry level lower concentration support employment growth. Less competition rather than higher competition promotes more job creation and city growth, and diversity within the structure of the city economy is desirable. This supports the dynamic Jacobs’ externalities argument, which states that knowledge spillovers accrue through contact of various economic agents or professionals in a specific spatial setting. This also implies that city-industries prosper where more industrial diversity exists in a particular city, because this makes the exchange of inter-industry knowledge easier.
However, after controlling for city-specific and industry-specific characteristics, the results change significantly. City-industry concentration was found to be not statistically significant, while less diversity in the city industrial environment became statistically significantly positive. These results are very intriguing as it supports neither the MAR externalities nor Jacobs’ externalities theories. A possible explanation for the difference in the research results may be that different levels of development may cause differences in city-industry growth rates.
The unique city-industry and city characteristic therefore seem very relevant in terms of city-industry and city employment growth that is not necessary linked to knowledge spillovers. Knowledge spillovers may therefore only be one of the primary reasons why some city-industries grow or decline. This suggests that further research is needed to unearth these unique factors that can explain the growth experience of city-industries.
Acknowledgements
The authors acknowledge the support from the World Trade Organization (WTO) and the National Research Foundation (NRF). Opinions expressed and conclusions arrived at in the article are those of the authors and should not necessarily be attributed to these institutions.
Competing interests
The authors declare that they have no financial or personal relationships which may have inappropriately influenced them in writing this article.
Authors’ contributions
C.E.C. designed the original concept and analysis. E.P.J.K. assisted in the composition and wrote the final article.
References
Alonso, W., 1960, ‘A theory of the urban land market’, Papers in Regional Science 6(1), 149–157. https://doi.org/10.1111/j.1435-5597.1960.tb01710.x
Arrow, K.J., 1962, ‘The economic implications of learning by doing’, Review of Economic Studies 29(3), 155–173.
Beckmann, M., 1969, ‘On the distribution of urban rent and residential density’, Journal of Economic Theory 1(1), 60–67. https://doi.org/10.1016/0022-0531(69)90012-X
Bernstein, A. & McCarthy, J., 2005, ‘Thinking big in small-town South Africa’, Business Day, 05 August, p. 15.
Blein, U. & Suedekum, J., 2005, Local economic structure and industry development in Germany, Discussion Paper No.1/2005, Institute for Employment Research (IAB), Nuremberg.
Borts, G., 1960, ‘The equalization of returns and regional economic growth’, American Economic Review 50(3), 319–347.
Button, K., 1998, ‘Where did the “New Urban Economics” go after 25 years?’, Paper presented at the 38th Congress of the European Regional Science Association, Vienna, 28th August–01st September.
Camagni, R., 1992, ‘Development scenarios and policy guidelines for the lagging regions in the 1990s’, Regional Studies 26(4), 361–374. https://doi.org/10.1080/00343409212331347051
Central Statistical Service (CSS), 1996, Living in South Africa, selected findings of the 1995 October household survey, CSS, Pretoria, 44p.
Chinitz, B., 1962, ‘Contrasts in agglomeration: New York and Pittsburgh’, American Economic Review, Papers and Proceedings 52, 279–289.
Courtney, P., Lépicier, D. & Schmitt, R., 2005, ‘Rural firms and the local economy – A focus on small and medium-sized towns’, in 45th Congress of the European Regional Science Association (ERSA), Vrije Universiteit Amsterdam, Amsterdam, August 23–27.
Duranton, G. & Puga, D., 1999, Diversity and specialisation in cities: Why, where and when does it matter? Research Papers in Environmental and Spatial Analysis no. 56, London School of Economics: Department of Geography & Environment, London.
Eckey, H.-F. & Kosfel, R., 2004, New economic geography, Volkswirtschaftliche Diskussionsbeiträge no. 65, Fachbereich Wirtschaftswissenschaften, Universität Kassel, Kassel.
EuroStat, 2017, Glossary of statistical terms, viewed 24 July 2017, from http://stats.oecd.org/glossary/detail.asp?ID=1178
Fujita, M. & Mori, T., 2005, ‘Frontiers of the new economic geography’, Papers in Regional Science 84(3), 377–405. https://doi.org/10.1111/j.1435-5957.2005.00021.x
Glaeser, E.L., Hedi, D., Scheinkman, J.A. & Schleifer, A., 1992, ‘Growth in cities’, Journal of Political Economy 100(6), 1126–1152. https://doi.org/10.1086/261856
Glaeser, E.L., Scheinkman, J. & Shleifer, A., 1995, ‘Economic growth in a cross-section of cities’, Journal of Monetary Economics 36(1), 117–143. https://doi.org/10.1016/0304-3932(95)01206-2
Global Insight, Southern Africa, 2017, Regional explorer rex-database, viewed 24 July 2017, from http://www.globalinsight.co.za
Isard, W., 1956, Location and space-economy, MIT, Boston, MA.
Jacobs, J., 1969, The economy of cities, Vintage, New York.
Kain, J. & Neidercorn, D., 1963, ‘An econometric model of metropolitan development’, Papers in Regional Science 11(1), 123–143.
Kleynhans, E.P.J., 2006, ‘The role of human capital in the competitive platform of South African industries’, South African Journal of Human Resource Management 4(3), 56–63. https://doi.org/10.4102/sajhrm.v4i3.100
Kleynhans, E.P.J., 2016, ‘Determinates of industrial competitiveness and the role of spillovers’, Journal of Applied Business Research 32(2), 527–540. https://doi.org/10.19030/jabr.v32i2.9594
Kleynhans, E.P.J. & Drewes, J.E., 2008a, ‘The influence of location on the efficiency of manufacturers in South Africa’, Town and Regional Planning 53, 1–8.
Kleynhans, E.P.J. & Drewes, J.E., 2008b, ‘The influence of location on the international competitiveness of South African industries’, Journal of Economic and Financial Sciences 2(2), 139–158.
Kleynhans, E.P.J. & Swart, A., 2012, ‘Spillover effects enhancing sales, production and competitiveness of South African manufacturers’, African Journal of Business Management 6(10), 3699–3705.
Krugman, P., 1991, ‘Increasing returns and economic geography’, Journal of Political Economy 99(3), 483–499. https://doi.org/10.1086/261763
Krugman, P. & Venables, A.J., 1995, ‘Globalization and the inequality of nations’, Quarterly Journal of Economics 110(4), 857–880. https://doi.org/10.2307/2946642
Lu, Y., Ni, J., Tao, Z. & Yu, L., 2013, ‘City-industry growth in China’, China Economic Review 27, 135–147. https://doi.org/10.1016/j.chieco.2013.08.004
Lucas, R.E., 1988, ‘On the mechanics economic development’, Journal of Monetary Economics 22(1), 3–42. https://doi.org/10.1016/0304-3932(88)90168-7
Luus, M. & Krugell, W.F., 2005, ‘Economic specialisation and diversity of South Africa’s cities’, Paper presented at the Biennial Conference of the Economic Society of South Africa, Durban, 7–9th September.
Marshall, A., 1890, Principles of economics, Macmillan, London.
McGregor, R.R. & Liner, G.H., 2002, ‘Municipal economic growth, 1960–1990’, Quarterly Journal of Business and Economics 41(1/2), 105–116.
Mills, E.S., 1995, ‘Projecting growth of metropolitan areas’, Journal of Urban Economics 37(3), 344–360. https://doi.org/10.1006/juec.1995.1018
Muth, R., 1961, ‘The spatial structure of the housing market’, Papers in Regional Science 7(1), 207–220. https://doi.org/10.1007/BF01969081
Muth, R.F., 1969, Cities and housing, University of Chicago Press, Chicago, IL.
Nijkamp, P., 2008, ‘XXQ factors for sustainable urban development: A systems economics view’, Romanian Journal of Regional Science 2(1), 1–34.
Nijkamp, P., 2009, ‘Cities as self-organizing innovative complexes’, in M. De Noronha Vaz (ed.), Innovation for development, Faro University of Algarve, Faro.
Porter, M.E., 1998, The competitive advantage of nations; with a new introduction, Palgrave, New York.
Romer, P., 1986, ‘Increasing returns and long-run growth’, Journal of Political Economy 94(5), 1002–1037. https://doi.org/10.1086/261420
Statistics South Africa (StatsSA), 2016, Community survey 2016 Statistical Release 0301, StatsSA, Pretoria.
Von Thünen, J.H., 1842, Die isolierte Staat in Beziehung auf Landwirtshaft und Nationalökonomie, Pergamon Press, Rostok.
|

