Abstract
Orientation: The 2007–2008 global financial crisis caused negative spillovers to the real economy of the United States as well as other economies across the world.
Research purpose: The main aim of this article is to determine the cyclical characteristics of important South African financial sections.
Motivation for the study: Financial cycles are complex, making them hard to measure and understand. This, in turn, makes financial cycles and the effect of fluctuations in financial cycles hard to predict and manage.
Research design, approach and method: Principal component analyses were used to construct an index for these South African financial sections. The Christiano–Fitzgerald (CF) band-pass filter was used to extract cycles from these South African financial indexes. Finally, spectral density analysis was used to characterise the cyclical duration exhibited by each South African financial section. The time horizon of this study ranges from 01/01/1975 to 01/12/2017, a 42-year period.
Main findings: The analysis showed that the South African credit cycle has the longest duration among all the South African financial sections and has a duration longer than that of the traditional business cycle. The cycles of other South African financial sections provided no clear evidence of durations longer than the traditional business cycle. Furthermore, South African interest rate conditions and South African economic confidence measures exhibit the largest amplitude.
Practical/managerial implications: The findings of this study can be used to enhance the efficiency of policies to manage cyclical fluctuations of important South African financial cycles and help other economic participants to anticipate cyclical fluctuations and thereby manage the potential effects of such fluctuations.
Contribution/value-add: The results in this study therefore offer value to both policymakers and other economic participants, such as asset managers, who need to make decisions related to cyclical fluctuations in South African financial conditions.
Keywords: financial cycles; spectral density analysis; principal component analysis; Christiano–Fitzgerald filter.
Introduction
The main aim of this study is to extract and characterise the cyclical behaviour of important financial sections in the South African economy, based on a wide range of South African financial variables. The 2007–2008 global financial crisis caused negative spillovers to the real economy of the United States as well as other economies across the world. Financial factors used to be an afterthought for policymakers at one point but are now a point of debate in policymaking (Chorafas 2015; Schüler, Hiebert & Peltonen 2017). The important role financial factors can play in the path of the real economy, and the potential disruption it can cause if neglected, has become apparent in recent years. As a result, policymakers realised that financial factors cannot simply be left to progress completely on its own path, nor can it be controlled by simply controlling the real economy, giving rise to the concept of macroprudential policies (Borio 2014).
Cyclical fluctuations in real economic activity are typically proxied by the business cycle, and the business cycle could be measured in terms of gross domestic product (GDP). GDP therefore aids as a simplistic measure for policymakers and other economic agents to measure the stance of the real economy and manage it accordingly. This, however, is not the case for the financial side of the economy. There are a vast number of financial variables that can potentially be used to measure the financial climate of an economy, and therefore just as many potential variables for policymakers to manage. One of the major challenges in macroprudential policymaking is to determine how the cycles of these vast number of financial components should be managed (Galati & Moessner 2013). Macroprudential policy is an overarching concept for a set of policies that aims to foster financial stability (Galati & Moessner 2013).
Galati and Moessner (2013) argue that the above-mentioned debate prevails because of the lack of research and knowledge regarding the cyclical characteristics of the important prevailing financial cycles in an economy. This is particularly the case of emerging economies, such as the South African economy. The bulk of research work on South African economic cycles focuses on the business cycle, such as the work by Botha, Greyling and Marais (2006), Du Plessis (2004) and Moolman (2004), and very little work has been conducted on South African financial cycles. In order for South African policymakers and other economic participants to fully understand cyclical movements in the South African economy, the body of academic literature on South African financial cycles needs to grow.
A potential means to address the complexity of financial cycles, which is largely caused by the large amount of potentially significant financial variables, is to group the large number of financial variables present in an economy into a small number of common sections. This will allow one to aggregate the cyclical behaviour of a large number of variables into a limited number of representing financial sections. This will allow policymakers to focus on a limited number of aggregate cyclical measures rather than a large number of individual variables (Menden & Proano 2017).
There are three key objectives that accompany the main aim of this study. The first objective is to construct a representing index for important South African financial sections. The second objective is to extract the trend component from each representing index to identify a representing cycle for each South African financial section. And the third objective is to characterise the cyclical behaviour of each cycle and compare the cyclical behaviour between important financial cycles and the South African business cycle
The motivation for this study is that financial cycles are complex, making it hard to measure and understand. This, in turn, makes financial cycles and the effect of fluctuations in financial cycles hard to predict and manage. Fluctuations in financial cycles also proved to be extremely disruptive, emphasising the need to improve the understanding of these cycles. This study will afford the measurement of South African financial cycles to be simplified and improve the understanding of South African financial cycles. This study will therefore aid in the understanding of financial cycles which proved over the past decade to be complex, because of magnitude, as well as disruptive. Better understanding South African financial cycles and having a more simplistic frame of reference will improve the ability of South African policymakers and other economic participants to make decisions related to financial cycle, such as interest rate decisions, asset allocation decisions and fixed capital formation decisions.
Asset managers can, for example, take the typical duration and amplitude of South African interest rate cycles to determine where in the cycle current interest rates are and thereby determine whether interest rates are likely to rise or fall. The same can be done for the South African credit cycle or the South African equity cycle. Policymakers can, for example, use the characteristics of South African credit cycles extracted in this study to determine whether credit is overextended or not. The value of this study therefore lies in the simplification and understanding of South African financial cycles, which will, in turn, make fluctuations in financial cycles more manageable.
Hereafter the study will follow the following structure: firstly, an overview of relevant literature will be provided. Secondly, the data to be used in this study and the methodology to be utilised in this study will be described.
Literature review
The literature on financial cycles has grown since the financial crisis of 2007 or 2008. The realisation came about that aggregate financial cycles are not simply a sole function of the real economy, but often a self-reinforcing cycle typically driven by subjective value perceptions, risk appetite and fluctuating financing constrictions by market partakers (Menden & Proano 2017). This realisation prompted research in the field of financial cycles. However, despite the growth in literature on financial cycles, no agreed upon definition for financial cycles exist yet, making it a challenge to know what exactly to consider when considering financial cycles (Adarov 2018; Aikman, Haldane & Nelson 2015; Borio 2014; Claessens, Kose & Terrones 2012; Pontines 2017; Schüler et al. 2017). In literature, a number of researchers have proposed definitions for the aggregate financial cycle. Borio (2014) proposed that financial cycles are the interface between the change in perceived value and risk of assets, a change in the level of available financing and the level of liquidity prevailing in the market, resulting in upwards and downwards movements in these cycles. Ng (2011) suggested a similar definition, stating that financial cycles are variations in the perception and appetite for risk over time, typically driven by fluctuations in credit levels, asset prices and available funding.
By these definitions, cyclical fluctuations in financial conditions cannot be summed up and proxied by a single variable. This infers that cyclical characteristics of a number of variables need to be considered for one to fully understand cyclical fluctuations in financial conditions (Claessens et al. 2012). Despite this, Menden and Proano (2017) state that most financial cycle research focuses on a small number of variables to proxy aggregate financial cycles, and neglect to consider and incorporate the vast number of financial variables that can potentially have an effect on aggregate economic conditions. Farrell and Kemp (2017), Pontines (2017), Aikman et al. (2015), Borio (2014) and Claessens et al. (2012) are examples of research work that only considered credit cycles and property price cycles as measures of aggregate financial cycle conditions. Yet, it cannot simply be assumed these parsimonious variables will always be the most accurate way to represent the dynamics of a financial cycle. Given the disruptive nature of cyclical fluctuations in financial conditions, it can be argued that it is essential to have the best possible understanding of the aggregate financial cycle, to provide the best change for policymakers to effectively manage the aggregate financial cycle.
A number of researchers, such as Hiebert, Jaccard and Schüler (2018), Adarov (2018), Chorafas (2015), Borio (2014) and Sarbjin (2014), have studied the characteristics of financial cycles in developed economies, and the common consensus is that financial cycles typically have a duration of 8–32 years, a much longer duration than that of business cycles, but that equity cycles typically have a duration of 2–8 years, in line with that of the typical business cycle. Furthermore, Hiebert et al. (2018) and Borio (2014) found that financial cycles typically exhibit cycles with an amplitude much larger than that of the typical business cycle. Claessens et al. (2012), however, found that the characteristics of financial cycles in emerging markets are considerably different than that of developed markets.
Pontines (2017) and Claessens et al. (2012) found evidence that the financial cycles of developing countries are much shorter and sharper than that of developed countries. Borio and Drehmann (2011) state that this can have various modelling implications, such as a misspecification of band-pass filter durations, indicating that consideration should be given to these differentials when extracting cycles using band-pass filters.
Some work has been conducted on the South African financial cycle, such as the work by Farrell and Kemp (2017) and Boshoff (2005). However, these researchers have proxied the South African financial cycle with a very limited number of financial variables, neglecting to consider the vast potential financial variables that could have an essential role in financial conditions. Farrell and Kemp (2017), for example, only measured the South African financial cycle in terms of South African credit levels, house prices and aggregate equity prices. Similarly, Boshoff (2005) also proxied the South African financial cycle in terms of credit levels and house prices. Existing research on South African financial cycles neglects to consider essential financial variables such as South African interest rate conditions, bank balance sheet conditions and foreign financial conditions. These financial aspects are identified by the literature to be important financial aspects (Menden & Proano 2017; Schüler, Hiebert & Peltonen 2015).
Characterising and understanding the cycles of all the financial aspects of an economy will afford policymakers a more thorough and full view of aggregate South African financial conditions. It will also allow other economic participants to distinguish between the characteristics of important financial cycles. This will allow economic participants to focus on the cyclical characteristics of variables most relevant to their operations. Filling this research gap will, thus, make an economic policy contribution and afford other economic agents the knowledge to better manage relevant financial cyclical fluctuations.
Methodology and data
Data description
In this study, the cyclical characteristics of seven South African financial sections are determined. These sections are South African credit conditions, South African property market conditions, South African interest rate conditions, balance sheet conditions of the South African financial sector, South African equity market conditions, South African economic confidence levels and South African foreign financial positions.
South African credit conditions consist of variables that measure credit levels in South Africa, such as total private domestic credit extended and total credit to government. It also includes variables related to credit extension and contraction such as money supply. South African property market conditions consist of variables that measure aggregate South African house prices. South African interest rate conditions consist of variables that measure the cost of money in the South African economy, variables that measure the spread between the cost of money given different borrowing durations and the spread between the cost of money given different credit qualities. Note that interest rate spreads are calculated by means of calculating the difference between the yield of a debt instrument with a relatively longer duration and the yield of a debt instrument with a relatively shorter duration. Also, note that the quality yield spread is calculated by means of determining the difference between the yield on a South African government bond and a government bond of the United Sates with similar maturities.
Balance sheet conditions of the South African financial sector consist of variables that measure the aggregate state of the balance sheet of South African financial institutes, such as total bank assets, total bank liabilities and liquid assets by banks. South African equity market conditions consist of variables that measure aggregate South African equity prices as well as equity prices of specific industries in South Africa. Furthermore, variables measuring dividend yield offered by equity in South Africa are included in this section. South African economic confidence levels include variables that indicate the level of confidence in the South African economy, such as business confidence, consumer confidence and gross capital formation. Finally, South African foreign financial positions consist of variables that measure key foreign financial positions, such as total foreign assets held by the South African Reserve Bank, total gold and foreign exchange reserves at the South African Reserve Bank and non-resident purchases of South African shares and bonds.
The full lists of variables that constitute each financial section are listed in the Appendix 1, Table 1-A1. The time horizon of each variable to be included in the analysis ranges from 01 January 1975 to 01 December 2017, a 42-year period, and the frequency of the data is monthly. Both the Thompson Reuters Datastream database as well as the Quantec database are utilised to gather the relevant data for this study. In circumstances where the variable does not date back to 01 January 1975, multiple imputation will be used to simulate these data points. Van Ginkel and Kroonenberg (2017) state that multiple imputation relies on estimating missing data points multiple times based on prevailing patterns between the variable with the missing data and the other variables without missing data points. This process typically reduces errors and improves validity and robustness, relative to other imputation methods, because of the fact that the method does not only rely on a single imputation, but also on the average of a number of imputations (Van Ginkel & Kroonenberg 2017). A relatively more robust interpolation approach will increase the accuracy of each cycle estimated in this study.
Another issue is frequency mismatches between variables, for example some variables are only released on a quarterly basis. In such cases, cubic spline interpolation methodology will be used to transform frequency mismatches. Brooks (2008) argues that the cubic spline interpolation methodology typically provides an interpolating polynomial with less errors and that is less erratic and smoother than other well-known interpolation methods. Provided that the aim of this study is to extract smooth cycles for important South African financial sections, it will be optimum to implement cubic spline interpolation methodology, given that this methodology is known to provide a relatively smoother polynomial.
Methodology
Principal component analysis
Economic and financial variables typically exhibit syncretic movement among each other. Because of the correlation among economic and financial variables, it is argued that a set of observable variables can be compressed into a limited number of representing latent variables and thereby aid as a means of dimension reduction (Stock & Watson 2006). Pearson (1901) developed the principal component analysis (PCA) framework which is a well-known dimension reduction technique (Stock & Watson 2006). Brooks (2008) states that a PCA is a dimension reduction procedure that uses correlation among observable variables to orthogonally transform a range of variables into one or two principal components. In other words, a PCA transforms a set of variables that are potentially correlated into a limited number of uncorrelated variables that are called principal components. The aim is to encapsulate a maximum amount of variance among variables into as few as possible principal components.
Brooks (2008) and Stock and Watson (2006) state that a PCA works well when working with a large group of variables that can naturally be divided into pre-specified groups. This is in contrast to the dynamic factor model that only allows for a limited number of variables. The PCA is an ideal dimension reduction technique for this study given that 73 financial variables will be considered and subdivided in this study. Therefore, to reduce all the representing variables of a given South African financial section into a representing index, a PCA will be used. The principal components are independent linear combinations of the primary data and can be specified as follows (Pearson 1901):
where p1 represents the first principal component, followed by pk as principal components. The original variables are represented by x1 to xk and α are the component loadings, showing the correlation between the principal component and the variable. More specifically, because the eigenvectors determine the weights of each principal component, a vector of eigenvalues e1 to ek can be used to re-specify the above equation.
where
Principal component is determined based on its eigenvalue which is derived from the variance matrix, and the first principal component encapsulates the maximum variance of the underlying variables, and therefore the largest eigenvalue. Brooks (2008) suggests that components with eigenvalues equal or larger than 2 are worthwhile considering. The reasoning behind this is that components with eigenvalues equal to or larger than 2 aid as a latent factor for at least two variables.
Furthermore, Lansangan and Barrios (2009) showed that PCA renders more accurate result if the input variable is stationary. Therefore, as suggested by Lansangan and Barrios (2009), non-stationary variables will be transformed to stationary variables by means of differencing the time series. The unit root test outputs for each variable included in this study are depicted in the Appendix 1, Table 1-A1. Furthermore, the Kaiser (1958) Varimax rotation will be applied to each PCA in this study to maximise the component loadings of each variable to the first principal component. The Kaiser (1958) Varimax rotation method creates a more simplistic state space structure, thereby improving the interpretability of component loadings and reducing the possible ambiguity.
Index weighting scheme
To construct a single index, given a range of variables, a weighting scheme needs to be determined (Elliot & Timmermann 2013). Chao and Wu (2017) outlined a framework according to which an index can be built based on PCA loadings. Lansangan et al. (2009) state that a principal component is a weighted sum of all the input variables weighted by each variable’s component loading. Therefore, component loadings can be effectively used as a weighting scheme to construct an index. The manner in which the weighting of each variable towards the index of a corresponding South African financial section is calculated will differ slightly depending on the number of components explaining that section. In the case where only one component has an eigenvalue larger than 2, and thus only one representing component, the weighting of a variable towards the index will be calculated as follows (Chao & Wu 2017):
where LX is the component loading of variable Xi onto the component and ∑Li is the sum of all the component loadings with an absolute value larger than 0.4. In a case where there are two common components with eigenvalues larger than 2, and thus two representing components, then the variables primarily loading onto the component with a higher eigenvalue should have a relatively higher weighting towards the index. Therefore, the component loading of each variable will first be relatively weighted based on the corresponding eigenvalue of the component a variable primarily loads on to. This will be done in accordance with the following equation:
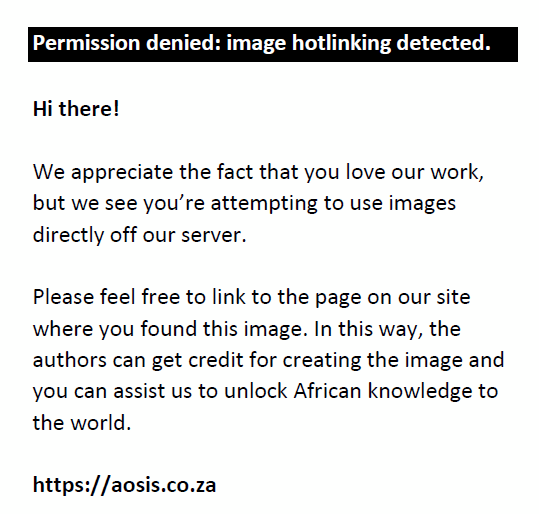
where L′X is the eigenvalue adjusted component loading for Xi, EVCPLX represents the eigenvalue of the component onto which variable Xi primarily loads onto and ∑EV>2 is the sum of all the eigenvalues larger than 2 because only components with an eigenvalue larger than 2 will be considered in the study. The following equation will be used to calculate the final weighting of variable Xi given a case where two common components are extracted.
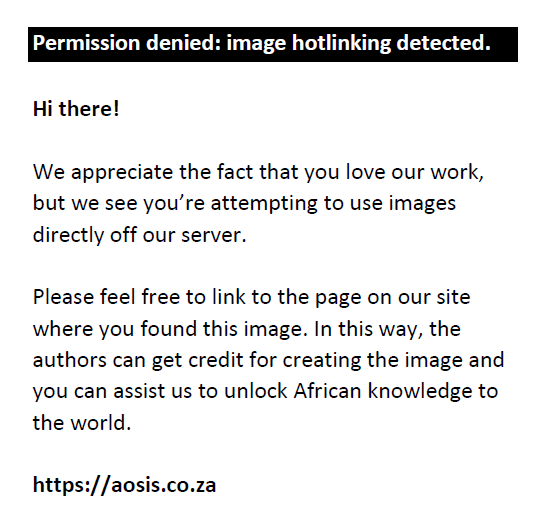
The index for a given financial section will then be calculated as follows:
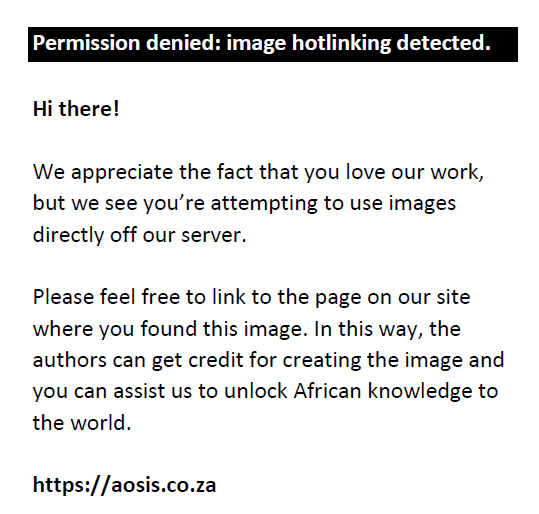
The index for a given South African financial section is therefore the component loading weighted sum of all the representing variable for that given financial section. Note that if a given variable Xi has a negative component loading, then WX in Equation 7 will be negative to encapsulate the inverse movement exhibited by variable Xi (Chao & Wu 2017). Note that the PCA is conducted only to establish the weight of each variable towards the corresponding index; therefore, even though the variables included in the PCA will be stationary, once the weight of each variable is determined with PCA, the original time series of a variable will be aggregated and thus a non-stationary index can exist.
Once an index has been constructed for each South African financial segment, the cycles will be extracted from each index to represent the cyclical movements of that specific financial segment.
Cyclical extraction: Christiano–Fitzgerald filter
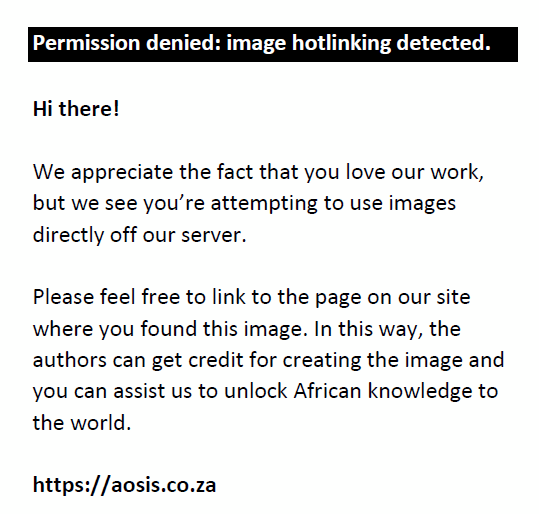
Some of the most regularly used filters in economic and econometric research to extract cycles is the Hodrick Prescott filter, the Baxter-King filter and the Christiano–Fitzgerald (CF) filter (Adarov 2018; Gomez 2001; Ravn & Uhlig 2002). It is often found, however, that the Hodrick Prescott filter picks up short-term noise in a stochastic process and therefore often produces spurious cycles (Woitek 1998). Furthermore, Nielsson (2011) states that the CF filter does not have a trimming factor like the Baxter-King filter, and therefore uses the total set of filtered data points. Nielsson (2011) argues that the asymmetric properties of the CF filter generally make the CF filter more accurate than the filter. The CF filter will therefore be used to extract representing cycles from each South African financial index. As specified by Christiano and Fitzgerald (2003), the CF filter can be calculated as follows:
where
where pu depicts the lower limit of the pre-specified cyclical duration period and pl depicts the upper limit of the pre-specified cyclical duration period. Any cycle that depicts a duration shorter than pu or longer than pl will be preserved in ct. Once the cycles for each South African financial sections have been extracted, spectral density analysis will be used to characterise these cycles. Pontines (2017) and Strohsal, Proano and Wolters (2015) are examples of researchers who have implemented spectral density analysis to characterise economic cycles.
Spectral density analysis
In this study, spectral density analysis will be implemented to characterise cycles within the frequency sphere. Spectral density analysis is based on the second momentum of a cyclical series and presents a way to extract and interpret information encapsulated in the second-order movement of a cyclical series. The spectrum of a cyclical series can be defined as the variance distribution of that series as a function of frequency (Strohsal et al. 2015). According to Strohsal et al. (2015), the autoregressive moving average (ARMA) model can be used to estimate the spectrum of a cyclical series. In accordance with Box and Jenkins (1976), the ARMA (p, q) process can be specified as follows:
where xi are the autoregressive terms in the model, with xt - p optimal lags, and et is the moving average term, with et - q optimal lags, and bq is the corresponding moving average coefficient. The frequency frontier for the spectrum of the ARMA process is between minus p and p and can be defined as follows in accordance with Pontines (2017):
where f shows the frequency of variance within a specific period, f(w) refers to the ARMA(p, i, q) spectrum and ai and bi are parameters substituted from the ARMA(p, i, q) process in Equation 9. By this equation it is shown that the ARMA(p, i, q) parameters determine the shape of the spectrum, but do not affect the frequency variance of a specific period.
In contrast to traditional time domain analysis techniques, which considers how the second movement of a series evolves and changes over time, spectral density analysis depicts the extent to which movement in a cyclical series lies within a specific frequency band (Pontines 2017). This allows one to establish the typical duration range of a cycle. Strohsal et al. (2015) state that the power of a cycle at frequency zero should be zero if a given filter totally removed the trend component from a series, for example one of Baxter and King’s (1999) objectives was to structure a band-pass filter that places a zero weighting at a zero frequency. The absence of cyclical power at a zero frequency will thus confirm whether a given filter was able to fully remove the trend of a series.
This analysis will provide three key measures that will be used in this study. The first measure is a special density level that indicates the frequency at which the volatility of a cycle peaks, as well as the cyclical duration that corresponds with that frequency level. This level will indicate the most prominent, and thus most common cyclical duration of a given cycle. The second measure will be a frequency band that indicates an upper and lower frequency level between which most of the spectral mass lies, and thus a cyclical duration band between which most of the volatility of a given cycle takes place. The third measure will show the percentage of total volatility within a cycle that takes place between the frequency band produced by the second measure. These measures will be used to identify the typical duration of a given cycle.
Results and findings
This analysis will start with determining the number of common components needed to represent each financial section of the South African economy by making use of the eigenvalues of each component (Brooks 2008). After establishing this, the PCA will be conducted, and the significance of conducting a PCA on a given set of representative variables will be determined based on the Kaiser–Meyer–Olkin (KMO) measure of sampling adequacy and the Bartlett’s test of sphericity (BTS) (Brooks 2008). Then the component loadings of each section’s representing variable onto the common component/s will be considered. These loadings will then be used to construct a representing index for each South African financial section. Following on from this, various filters will be used to extract cycles from the index that represents each South African financial section. Finally, spectral density analysis will be implemented as a means to determine the typical duration of each cycle.
Note that only components with eigenvalues larger than 2 will be considered. Based on the eigenvalue plots in Figure 1, it can be inferred that the following South African financial sections are encapsulated by one common component: credit conditions, property prices, South African economic confidence indicators, foreign financial position and bank balance sheet conditions. Furthermore, South African interest rate conditions and South African equity market conditions are encapsulated by two components. Given this optimum amount of representing components for each financial section, the analysis can carry on and the significance of implementing a PCA on a given set of variables can be assessed.
 |
FIGURE 1: Screen plot of the eigenvalues of each respective section. (a) South African credit conditions, (b) South African interest rate conditions, (c) South African house prices, (d) South African equity markets, (e) financial confidence indicators, (f) foreign financial positions, (g) bank balance sheet conditions. |
|
Evaluating the implementation of principal component analysis
Table 1 depicts the Kaiser–Meyer–Olkin (KMO) Measure and the p-value of the Bartlett test statistic for each South African financial section.
| TABLE 1: Kaiser-Meyer-Olkin (KMO) statistic and p-value of Bartlett’s test statistic. |
Given that the KMO test results for each financial section depicted in Table 1 are all above 0.7, a reasonable proportion of the variance among variables representing each financial section of South Africa is adequately represented by a common component or components. Furthermore, based on the p-value of the Bartlett test statistic for each financial section, a significant portion of the variance among the variables in each section is homogenic.
Now the communalities of each variable and the relating underlying components are calculated and considered, as depicted in Appendix 1, Tables 1-A1 and 2-A1. Given these communalities, only variables with a communality factor of 0.40 or higher will be included in the model, and thus any variables with a communality factor lower than 0.40 will be excluded from the study. In cases where variables are eliminated the calculation will be adjusted to normalise the total weighting of the index back to a 100%. After elimination of the necessary variables, a PCA analysis will be re-estimated. The eigenvalues of each respective component in each South African financial section are depicted in the Appendix 1, Table 3-A1.
Component loadings
The component loadings can simply be understood as the correlation between each observable variable and the corresponding components. Ideally, a variable should have a component loading larger than 0.4, which will indicate that a variable has a sufficient amount of homogenic movement in relation to the other observable variables (Brooks 2008).
Component loadings of South African credit conditions
Considering Table 2, all these variables load sufficiently and positively onto the first component. The positive synchronisation among South African credit measures and South African money supply aligns with the monetarist theory of economic cycles, which argues that a Central Bank of an economy increases money supply to encourage the extension of credit (Howard & Kolk 1996). The weightings of each variable towards the representing index are depicted in the right-hand column of Tables 2–8, and Equations 4–7 depict how these weightings are determined.
| TABLE 2: Component loadings of South African credit conditions. |
Component loadings of South African interest rate conditions
Given that South African interest rate conditions have two distinct components with eigenvalues larger than 2, two distinct groups of variables that exhibit co-movements exist. Considering individual loadings onto the first component represented in Table 3, the South African repo rate, the 3-month bankers’ acceptance rate, the inter-bank call money rate and the South African prime rate predominantly load onto this component. Furthermore, short-term government bond yields, and medium-term government bond yields also primarily load onto component 1. The component loadings are positive and indicate that these interest rates exhibit a strong to very strong co-movement among each other.
| TABLE 3: Component loadings of South African interest rate conditions. |
These findings concur with Lunsford (2018) in that short- to medium-term government bond yields are sensitive to changes in short-term interest rates such as the prime rate and the repo rate. On the contrary, South African long-term government bond yields proved to not have a strong co-movement with the other measures of interest rates and yields. This indicates that long-term debt is often disconnected from short-term interest rate changes, as suggested by Lunsford (2018). Based on these findings, long-term government bond yields will be excluded from this study and will only be used when calculating bond spreads.
Also, loading primarily onto component 1 is South African yield curve measures such as the yield spread between long-term and short-term South African government securities, medium-term and short-term South African government securities and the yield spread between long-term and medium-term South African government securities. These loadings are negative, indicating an inverse relationship with the component and the variables with positive component loadings. This finding relates to a large body of literature that studies the term structure of interest rates. Fama and French (1989) are examples of such work. These researchers found evidence that the yield curve is inversely related to economic activity in the short term.
Relating the yield curve with prevailing interest rate levels, Lunsford (2018) states that yield spreads tend to compress in a rising interest rate environment. The reasoning behind this is typically twofold. The first reason in that yields on short-term debt are typically more sensitive to Central Bank changes in interest rates (Fabozzi 2007). Thus, as interest rates rise because of monetary policy tightening, short-term yields tend to increase more than long-term yields (Fabozzi 2007). Secondly, as interest rates rise, prospects of future economic conditions decline and the return of future investments relative to the cost of borrowing diminishes. The demand for long-term credit will fall and can, as a result, cause long-term yields to decline (Fabozzi 2007). Both reasoning 1 and 2 will cause yield spreads to decline, and thus the yield curve to flatten. This argument provides a reasoning for why the loadings of the South African yield curve components load negatively onto component 1. Furthermore, the All bond price index also load negatively onto component 1. This is justified by the well-known concept that bond prices have an inverse relationship with interest rates (Fabozzi 2007). Lastly, component 2 almost solely represents yield spread between instruments with different credit quality such as SA-US short-term government yield spreads and SA-US medium-term government yield spreads. All three of these quality spread measures load positively and strongly onto the second component, indicating that the quality spread between all three durations moves together.
Component loadings of South African equity market conditions
South African equity market conditions also have two distinct components, and therefore two distinct groups of variables that exhibit co-movements. Considering individual loadings onto the first component represented in Table 4, all the South African equity indices primarily load positively onto one component. This indicates that an increase in the principal component represents an increase in each individual variable. This shows that share prices of various South African sectors exhibit syncretic movements and can be aggregated into one representing index that will encapsulate a large percentage of the variance of these variables.
| TABLE 4: Component loadings of South African equity market conditions. |
The second component represents various dividend yield measures such as the All share dividend yield measure, industrial dividend yield measure, resource dividend yield index and the financial dividend yield measure. These measures of dividend yield of various industries exhibit strong positive loadings. It is interesting that equity prices and dividend yields load onto two separate components, given a large body of literature suggesting that equity prices and dividend yields are closely related. However, given the weak loading of dividend yields onto component 1 which represents share price measures, the theory by Miller and Modgliani (1961) seems to be applicable in this case. Miller and Modgliani (1961) argued that share prices should reflect future dividend expectations because it is driven by known fundamental aspects of a company, and dividend changes should therefore have minimal effects on share prices.
Component loadings of South African house price conditions
Considering individual loadings onto the principal component represented in Table 5, it can be concluded that all three observable variables load highly positively onto the principal component extracted by the PCA.
| TABLE 5: Component loadings of South African house price conditions. |
Variance among this set of variables is thus highly correlated. This shows that property prices of various sizes in South Africa move together and can be aggregated into one index.
Component loadings of South African economic confidence indicators
Considering individual loadings onto the first component represented in Table 6, business confidence indicator, aggregate capacity utilised and the consumer confidence indicator load strongly onto component 1. These loadings are positive, suggesting that there is a positive co-movement among these three variables. The positive loading of aggregate capacity utilisation relates to the neoclassical theory on capacity utilisations which argues that an increase in the capacity utilisation rate stems from increases in economic demand which exceeds short-term supply (Greenwood, Hercowitz & Huffman 1988).
| TABLE 6: Component loadings for South African financial confidence levels. |
This is typically the case when an economy moves from a contraction or stagnate period to an expansion (Greenwood et al. 1988). A change in the capacity utilisation rate typically, therefore, indicates a change in economic sentiment and confidence. This is empirically supported by Santacreu (2016) who found that capacity utilisation rates are typically much higher during times of high economic confidence and economic expansion, relative to periods of lower economic confidence, as maximum capacity is needed to support higher economic demand.
Greenwood et al. (1988) state that the neoclassical framework argues that high capacity utilisation will eventually lead to an increase in capital investments, related to the positive loading that private fixed capital formation has on the common component. Therefore, as economic confidence rises and economic demand increases, the need for additional production capacity will lead to an increase in gross capital formation. In addition to this understanding, the Keynesian’s investment theory argues that capital investments will start to increase in anticipation of an economic upswing, and gross capital formation will therefore increase before an increase in demand if confidence in the economy is positive (Howard & Kolk 1996). Both the understanding stipulated by the neoclassical framework and the Keynesian’s investment theory explain the positive loading of gross fixed capital formation onto the extracted component loading that represents South African economic confidence.
Component loadings of South African bank balance sheet conditions
Table 7 depicts the component loadings of each respective observable variable included to represent South African bank balance sheet conditions to the common component extracted for this financial section. Based on the component loadings depicted in Table 7, it can be concluded that all the variables that proxy the balance sheet conditions of South African banks load strongly onto the common component. All the component loadings are positive, indicating that an increase in the principal component will represent an increase in all the underlying observable variables.
| TABLE 7: Component loadings of South African bank balance sheet conditions. |
The core business of retail banks is to receive deposits, reflected as liabilities on the balance sheet of a bank, and lend out the received deposits, which reflects as assets on the balance sheet of a bank (Gerali et al. 2010). By implication therefore, as bank liabilities increase, bank assets should also increase explaining the high positive component loadings exhibited by total bank liabilities and total bank assets.
Furthermore, Gerali et al. (2010) state that as total bank liabilities increase, and the economy expands, Central Banks typically increase the reserve requirement to control economic expansion and relatively high bank liability levels. This should typically lead to an increase in liquid assets held by banks, and total bank reserves at reserve bank, explaining the strong positive component loadings exhibited by these two variables.
Component loadings of South African foreign financial conditions
From Table 8, it is clear that all the variables in the South African foreign financial section have a positive component loading larger than 0.4. Movements in these variables are therefore fairly systematic, and an increase in the common component represents a general upwards movement in each respective variable.
| TABLE 8: Component loadings of South African foreign financial conditions. |
Constructed index and cycle for each South African financial section
In this section, the component loadings and eigenvalues identified in the previous section will be used to construct a representative index for each South African financial section. A full description on how component loadings and eigenvalues are used as a weighting scheme to construct an index for each South African financial section, and ultimately an aggregate South African financial conditions index is provided in the methodology section of this study. The values on the y-axes of the graphs in Figure 2 represent the index value of each respective South African financial section, and the value on the x-axes represents the time horizon in years.
 |
FIGURE 2: Index plots of important South African financial sections. (a) credit index, (b) interest rate index, (c) house price index, (d) equity index, (e) confidence index, (f) balance sheet index, (g) foreign position index. |
|
Visually analysing the index plots in Figure 2, South African credit conditions, house prices, equity price, bank balance sheet conditions and foreign financial positions all exhibit strong upward trends. Within the upward trends exhibited by these variables, cyclical fluctuations, thus fluctuations from the long-run trend, are however observable. This indicates that all these South African financial sections should exhibit cyclical movements. In contrast, the South African interest rate index and economic confidence index do not exhibit a clear trend, and the index as it is exhibits strong cyclical characteristics. Given these visual results, it is anticipated that South African interest rate cycles and economic confidence cycles will exhibit cycles with larger magnitudes than that of the other variables.
Figure 3 depicts the cycles that have been extracted from the index of each South African financial section. Each respective cycle therefore represents the cyclical behaviour of each financial section. The values on the y-axes of the graphs in Figure 3 represent the cyclical magnitude of each respective cycle and the value on the x-axes represents the time horizon in years.
 |
FIGURE 3: Cyclical extractions for each South African financial section. (a) credit cycle, (b) interest rate cycle, (c) house price cycle, (d) equity cycle, (e) confidence cycle, (f) balance sheet cycle, (g) foreign financial position cycle, (h) business cycle. |
|
It is clear that the CF filter has been able to extract smooth cycles for each financial section and was therefore able to eliminate the trend from each index. One can relatively compare the magnitude of each respective cycle by considering the y-axes of each graph. This indicates that South African economic confidence cycles exhibit cycles with the largest magnitude with cycles peaking at a magnitude close to 16, followed by South African interest rate cycles peaking close to 13. Compare these magnitude with that exhibited by equity cycles peaking close to 2.5 and credit cycles peaking at a magnitude of close to 0.7.
Given their relatively large magnitudes, South African economic confidence cycles and South African interest rate cycles are the most prominent cycles among all the South African financial sections. South African economic confidence cycles and South African interest rate cycles also have a larger magnitude than that exhibited by the South African business cycle; however, all the other South African financial cycles exhibit a smaller magnitude. A spectral density analysis will be used to further characterise and compare each South African financial cycle.
Figure 4 depicts the spectral densities exhibited by the cycles of each South African financial sections. By visually analysing these spectral densities, it seems like all the South African financial cycles have strength at fairly low frequencies, indicating that these cycles have fairly long durations. Furthermore, the spectral density plots indicate that all these cycles seem to have zero power at a zero frequency, indicating that the CF filter acted sufficiently in eliminating the trend component from each index. From these plots, it is very difficult to compare the cyclical durations of each South African financial cycle, and therefore the numerical results rendered by the spectral analysis will be considered.
 |
FIGURE 4: Spectral density plots for each South African financial cycles. (a) credit cycle, (b) interest rate cycle, (c) house price cycle, (d) equity cycle, (e) confidence cycle, (f) bank balance sheet cycle, (g) foreign financial position cycle. |
|
Table 9 depicts the numerical results from spectral density analysis. From these, it can be concluded that South African credit cycles have the longest cyclical duration, ranging from 7.5 years to 13.55 years. South African house price cycles and South African balance sheet cycles also exhibited relatively long durations ranging from 5.543 to 9.6 years and 4.248 to 9.982 years, respectively. On the relatively lower end of the duration scale are South African equity cycles and South African interest rates with a duration range of 2.75–5.48 years and 2.8–7.7 years, respectively. South African foreign position cycles and South African economic confidence cycles are interesting because of the large duration range spread exhibited by these two South African financial sections. Their duration peak of 4.289 and 5.428 years for South African economic confidence cycles and South African foreign position cycles, respectively, indicates short cyclical durations relative to South African credit cycles, South African house price cycles and South African balance sheet cycles. However, South African economic confidence cycles have an upper band of 9.869 years, and South African foreign position cycles have an upper band of 9.549 years. These upper bands compare with those exhibited by South African house price cycles and South African bank balance sheet cycles. This indicates that the cyclical duration of South African economic confidence cycles and South African foreign position cycles varies, and can at times be relatively short, and at times be relatively long. Furthermore, the cyclical density of South African interest rate condition cycles and South African economic confidence cycles confirms much higher than that of the other cycles. This provides additional evidence that South African interest rate condition cycles and South African economic confidence cycles have the largest amplitude.
| TABLE 9: Numerical results from spectral density analysis. |
These findings generally concur with findings by other researchers in the field, such as Pontines (2017), Borio (2014), Sarbjin (2014) and Claessens et al. (2012), in that credit cycles and house price cycles tend to be considerably longer than that of equity cycles. Note that the majority of studies characterising financial cycles of an economy only considered the cyclical duration of credit cycles, house price cycles and equity price cycles because these are known to be the most parsimonious components of an aggregate financial cycle. This limits the parallel that can be drawn between the findings in this study and the findings in literature regarding this matter.
Furthermore, the typical length of South African credit cycles concurs with the general notion that the duration of credit cycles is typically longer than that of the traditional business cycle (Claessens et al. 2012; Sarbjin 2014; Strohsal et al. 2015). However, cycles from other South African financial sections such as house prices, bank balance sheet positions and foreign financial positions have durations close to that of the typical business cycle, with only the upper duration bands of these cycles being slightly higher than the upper duration band of a typical business cycle. This does not correspond with the general view that financial cycle components have a longer duration than that of the business cycle. However, there is research, such as the research by Pontines (2017), that found empirical evidence that financial components and the aggregate financial cycle of emerging countries do not exhibit cyclical durations that are much longer than that of the business cycle. The findings by Pontines (2017) therefore relate to the duration of most of the South African financial components which exhibit cyclical durations similar to that of the traditional business cycle. The duration in equity cycles is typically the exception in most empirical research, where the duration of equity cycles typically exhibits cyclical durations closely related to that of the business cycle (Claessens et al. 2012; Sarbjin 2014; Strohsal et al. 2015). The duration of South African equity cycles corresponds with such findings.
Conclusion
The main aim of this article was to determine the cyclical characteristics of important South African financial sections. The main findings of this article are that cycles in South African economic confidence and cycles in South African interest rate conditions exhibit the highest amplitude among all the South African financial sections. The cyclical amplitude of these cycles also proved to be higher than that of the South African business cycle. This conforms to the findings of Borio (2014) that found financial cycles to typically exhibit cycles with an amplitude much larger than that of the typical business cycle. The amplitude of the South African equity cycles is fairly in line, but slightly lower than that of the South African business cycle. However, the amplitude of the cycles exhibited by other South African financial sections proved to be much lower than that of the South African business cycle. Furthermore, South African credit cycles have the longest cyclical duration, ranging from 7.5 to 13.55 years. This concurs with the general notion that the duration of credit cycles is typically longer than the well-documented 2–8-year duration exhibited by the traditional business cycle (Claessens et al. 2012; Sarbjin 2014; Strohsal et al. 2015). South African house price cycles and South African balance sheet cycles also exhibited relatively long durations ranging from 5.543 to 9.6 years and 4.248 to 9.982 years, respectively. In contrast, cycles of other South African financial sections provided no clear evidence of cycles exhibiting durations longer than the business cycle. This does not correspond with the general view that financial cycle components have a longer duration than that of the business cycle. However, there is research, such as the research conducted by Pontines (2017), that found empirical evidence that financial components and the aggregate financial cycle of emerging countries do not exhibit cyclical durations that are much longer than that of the business cycle.
The findings in this study add to the body of literature on financial cycles by proving information on the characteristics of South African financial cycles and provide a means to reduce a large number of South African financial variables to seven representing cycles. This information can be used to enhance the efficiency of policies to manage cyclical fluctuations of important South African financial cycles and help other economic participants to anticipate cyclical fluctuations and thereto manage the potential effects of such fluctuations. The results in this study therefore offer value to both policymakers and other economic participants, such as asset managers, who need to make decisions related to cyclical fluctuations in South African financial conditions.
Acknowledgements
Competing interests
The authors declare that they have no financial or personal relationships that may have inappropriately influenced them in writing this article.
Authors’ contributions
M.C.d.W. wrote the article. I.B. helped with the econometric modelling and provided input into the literature part of the article.
References
Adarov, A., 2018, Financial cycles around the World, Working paper, Vienna Institute of International Economic Studies, No. 145, Vienna, Austria.
Aikman, D., Haldane, A.G. & Nelson, B.D., 2015, ‘Curbing the credit cycle’, The Economic Journal 125(585), 1072–1109. https://doi.org/10.1111/ecoj.12113
Baxter, M. & King, R.G., 1995, Measuring business cycles. Approximate band-Pass filters for economics time series, Working Paper: National Bureau of Economic Research, No 5022, Cambridge, MA.
Borio, C., 2014, ‘The financial cycle and macroeconomics: What have we Learnt?’, Journal of Banking and Finance 45, 182–198. https://doi.org/10.1016/j.jbankfin.2013.07.031
Borio, C. & Drehmann, M., 2011, ‘Financial instability and macroeconomics: Bridging the Gulf’, World Scientific Studies in International Economics 14, 237–268. https://doi.org/10.1142/9789814322096_0017
Boshoff, W.H., 2005, ‘The properties of cycles in South African financial variables and their relation to the business cycle’, South African Journal of Economics 73(4), 694–709. https://doi.org/10.1111/j.1813-6982.2005.00047.x
Botha, I., Greyling, L. & Marais, D.J., 2006, ‘Modelling the business cycle of South Africa: A non-linear approach’, Journal of Studies in Economics and Econometrics 30(2), 103–126.
Box, G.E.P. & Jenkins, G.M., 1976, Time Series Analysis: Forecasting and controlling, Holden-Day, San Francisco, CA.
Brooks, C., 2008, Introductory Econometrics for Finance, 2nd edn., Cambridge University Press, Cambridge.
Chao, Y. & Wu, C., 2017, ‘Principal component-Based weighted indices and a framework to evaluate indices: Results from the medical expenditure panel survey 1996 to 2011’, PLOS One 12(9), 1–20. https://doi.org/10.1371/journal.pone.0183997
Chorafas, D.N., 2015, Financial cycles: Sovereigns, bankers and stress tests, Palgrave Macmillan, New York.
Christiano, L. & Fitzerald, T., 2003, ‘The Band-Pass filter’, International Economic Review 44(2), 435–465. https://doi.org/10.1111/1468-2354.t01-1-00076
Claessens, S., Kose, M.A. & Terrones, M.E., 2012, ‘How do business cycles and financial cycles interact?’, Journal of International Economics 87, 178–190. https://doi.org/10.1016/j.jinteco.2011.11.008
du Plessis, S., 2004, ‘Stretching the South African business cycle’, Economic Modelling 21(4), 685–701. https://doi.org/10.1016/j.econmod.2003.09.006
Elliot, G. & Timmermann, A., 2013, Handbook of economic forecasting, 2nd edn., North Holland, Amsterdam.
Fabozzi, J.F., 2007, Fixed income analysis, 2nd edn., John Wiley & Sons Inc, Hoboken, NJ.
Fama, F.F. & French, K.R., 1989, ‘Business conditions and expected returns on stocks and bonds’, Journal of Financial Economics 25, 23–49. https://doi.org/10.1016/0304-405X(89)90095-0
Farrell, G. & Kemp, E., 2017, Measuring the financial cycle in South Africa, viewed n.d., from SSRN: https://papers.ssrn.com/abstract=3079369
Galati, G. & Moessner, R., 2013, ‘Macro-prudential policy – A literature review’, Journal of Economic Surveys 27(5), 846–878.
Gerali, A., Neri, S., Sessa, L. & Signoretti, F.M., 2010, ‘Credit and banking in a DSGE model of the Euro Area’, Journal of Money, Credit and Banking 42, 107–141. https://doi.org/10.1111/j.1538-4616.2010.00331.x
Gomez, V., 2001, ‘The use of Butterworth Filters for trend and cycle estimation in economic time series’, Journal of Business and Economic Statistics 19(3), 365–373. https://doi.org/10.1198/073500101681019909
Greenwood, J., Hercowitz, Z. & Huffman, G., 1988, ‘Investment, capacity utilization, and real business cycle’, American Economic Review 78 (3), 402–417.
Hiebert, P., Jaccard, I. & Schüler, Y.S., 2018, ‘Contrasting financial and business cycles: Stylized facts and candidate explanations’, Journal of Financial Stability 38, 72–80. https://doi.org/10.1016/j.jfs.2018.06.002
Howard, J.S. & Kolk, D., 1996, Business cycles and forecasting, Harper College, New York.
Kaiser, H.F., 1958, ‘The Varimax Criterion for analytic rotation in factor analysis’, Psychometrika 23, 187–200. https://doi.org/10.1007/BF02289233
Lansangan, J.R.G. & Barrios, E.B., 2009, ‘Principal component analysis of nonstationary time series data’, Statistics and Computing 19(2), 173–187. https://doi.org/10.1007/s11222-008-9082-y
Lunsford, K.G., 2018, Can yield curve inversion be predicted? Economic Commentary, No. 385: Federal Reserve Bank of Cleveland, Cleveland, OH.
Menden, C. & Proano, C.R., 2017, Dissecting the financial cycle with dynamic factor models, Working paper 183, Monetary Policy Institute, University of Bamberg, Bamberg.
Miller, M.H. & Modgliani, F., 1961, ‘Dividend policy, growth, and the valuation of shares’, Journal of Business 34(4), 411–433. https://doi.org/10.1086/294442
Moolman, E., 2004, ‘A Markov switching regime model of the South-African Business Cycle’, Economic Modelling 21, 631–646. https://doi.org/10.1016/j.econmod.2003.09.003
Ng, T., 2011, The predictive content of financial cycle measures for output fluctuations, quarterly bulletin: Bank for International Settlements, Basel, Switzerland.
Nielsson, R., 2011, Cyclical extraction: A comparison of the phase-average trend method, the Hodric-Prescot and Christiano-Fitzgerald Filters, Working Paper: OECD Statistics Working Papers.
Ólafsson, T.T., 2016, ‘Financial cycle in Iceland Characteristics, spillovers, and cross-border channels’, 5th NBRM Research Conference, Central Bank of Iceland.
Pearson, K., 1901, ‘On the lines and planes of closest fit to systems of points in space’, Philosophical Magazine 2(11), 559–572. https://doi.org/10.1080/14786440109462720
Pontines, V., 2017, ‘The financial cycle in Four East Asian Economies’, Economic Modelling 65, 51–66. https://doi.org/10.1016/j.econmod.2017.05.005
Ravn, M.O. & Uhlig, H., 2002, ‘Notes on adjusting the Hodrick-Prescott filter for the frequency of observations’, The Review of Economics and Statistics 84(2), 371–380. https://doi.org/10.1162/003465302317411604
Santacreu, A.M., 2016, ‘Employment and capital utilization over the business cycle’, Economic Symposium 1(19), 1–2.
Sarbijan, M.S., 2014, ‘Modelling business cycles with Markov Switching ARMA (Ms-Arma) Model: An application on Iranian Business Cycles’, International Journal of Management, Accounting and Economics 3, 201–214.
Schüler, Y.S., Hiebert, P.P. & Peltonen, T.A., 2015, Characterising the financial cycle: A multivariate and time varying approach, Working paper, No 1846: European Central Bank, Frankfurt, Germany.
Schüler, Y.S., Hiebert, P.P. & Peltonen, T.A., 2017, Coherent Financial Cycles for G-7 Countries: Why Extending Credit can be an Asset, Working Paper: European Systematic Risk Board, No. 43.
Stock, J.H. & Watson, W., 2006, ‘Forecasting with many predictors, chapter 10’, Handbook of Economic Forecasting 1, 515–554.
Strohsal, T., Proano, C.R. & Wolters, J., 2015, Characterising the financial cycle: Evidence from a frequency domain analysis, Working Paper No. 22: Deutche Bundesbank, Frankfurt, Germany.
Van Ginkel, J.R. & Kroonenberg, P.M., 2017, ‘Evaluation of multiple-imputation procedures for three-mode component models’, Journal of Statistical Computation and Simulation 87(16), 3059–3081. https://doi.org/10.1080/00949655.2017.1355368
Woitek, U., 1998, A note on the Baxter-King Filter, Working Paper: University of Glasgow, Glasgow, Scotland.
Appendix 1
| TABLE 1-A1: Unit root test results for representing variables in each South African financial sections. |
|